Đề thi giữa HK1 môn Toán 10 CD năm 2022-2023
Trường THPT Đào Duy Từ
-
Câu 1:
Cho tập hợp A và a là một phần tử của tập hợp A. Trong các mệnh đề sau, mệnh đề nào sai?
A. {a} ⊂ A;
B. {a} ∈ A;
C. a ∈ A;
D. \(\emptyset \) ⊂ A .
-
Câu 2:
Cho mệnh đề chứa biến P(n): “n2 chia hết cho 4 ” với n là số nguyên. Chọn mệnh đề đúng trong các mệnh đề sau:
A. P(5);
B. P(2);
C. P(4);
D. P(6).
-
Câu 3:
Mệnh đề phủ định của mệnh đề “Phương trình ax2 + bx + c = 0 (a ≠ 0) vô nghiệm” là:
A. Phương trình ax2 + bx + c = 0 (a ≠ 0) không có nghiệm;
B. Phương trình ax2 + bx + c = 0 (a ≠ 0) có nghiệm;
C. Phương trình ax2 + bx + c = 0 (a ≠ 0) có 2 nghiệm phân biệt;
D. Phương trình ax2 + bx + c = 0 (a ≠ 0) có nghiệm kép.
-
Câu 4:
Gọi A là tập hợp các số thực không nhỏ hơn 1 và B là tập hợp các số thực có giá trị tuyệt đối nhỏ hơn 2. Tìm A∩B
A. A∩B=(1;2)
B. A∩B=[1;2)
C. A∩B=[1;2]
D. A∩B=(−2;1)
-
Câu 5:
Cho A = {0; 1; 2; 3; 4} và B = {2; 3; 4; 5; 6}. Tập hợp (A \ B) ∪ (B \ A) bằng?
A. {5; 6};
B. {2; 3; 4};
C. {1; 2};
D. {0; 1; 5; 6}.
-
Câu 6:
Số phần tử của tập hợp A = {k2 + 1| k ∈ ℤ, |k| ≤ 2} bằng
A. 1
B. 5
C. 3
D. 2
-
Câu 7:
Cho hai tập hợp (1; 3) và [2; 4]. Giao của hai tập hợp đã cho là
A. (2; 3];
B. (2; 3);
C. [2; 3);
D. [2; 3].
-
Câu 8:
Hình vẽ sau đây (phần không bị gạch) là biểu diễn của tập hợp nào?

A. (– ∞; – 2) ∪ [5; +∞);
B. (– ∞; – 2) ∪ (5; +∞);
C. (– ∞; – 2] ∪ (5; +∞);
D. (– ∞; – 2] ∪ [5; +∞).
-
Câu 9:
Lớp 10A1 có 6 học sinh giỏi Toán, 4 học sinh giỏi Lý, 5 học sinh giỏi Hóa, 2 học sinh giỏi Toán và Lý, 3 học sinh giỏi Toán và Hóa, 2 học sinh giỏi Lý và Hóa, 1 học sinh giỏi cả 3 môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) của lớp 10A1 là:
A. 15
B. 23
C. 7
D. 9
-
Câu 10:
Cặp số (x; y) nào sau đây là nghiệm của bất phương trình 5x – 3y ≤ 2?
A. (0; – 2);
B. (3; 0);
C. (2; 1);
D. (– 1; – 1).
-
Câu 11:
Bất phương trình nào sau đây không là bất phương trình bậc nhất một ẩn?
A. 8 – \(\sqrt{2}\)x ≤ 0;
B. 4x – 3 > 0;
C. \(\frac{1}{3}\)x – 3 < 0;
D. (x + 1)2 ≥ 1.
-
Câu 12:
Phần mặt phẳng không bị gạch chéo trong hình vẽ bên (kể cả biên) là biểu diễn hình học tập nghiệm của hệ bất phương trình nào dưới đây?
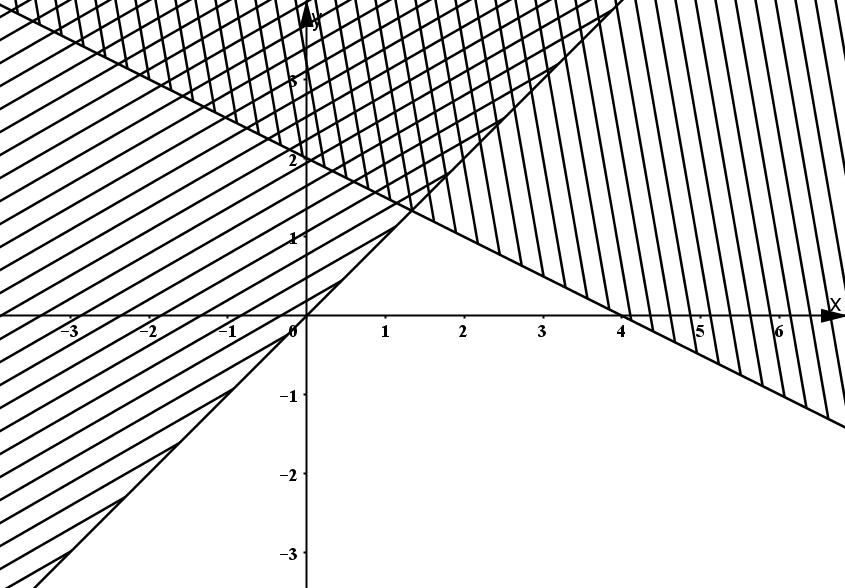
A. \(\left\{ {\begin{array}{*{20}{l}} {x - y \ge 0}\\ {x + 2y \le 4} \end{array}} \right.\)
B. \(\left\{ {\begin{array}{*{20}{l}} {x - y \le 0}\\ {x + 2y \ge 4} \end{array}} \right.\)
C. \(\left\{ {\begin{array}{*{20}{l}} {x - y \ge 0}\\ {x + 2y \ge 4} \end{array}} \right.\)
D. \(\left\{ {\begin{array}{*{20}{l}} {x - y \le 0}\\ {x + 2y \le 4} \end{array}} \right.\)
-
Câu 13:
Cho sin35° ≈ 0,57. Giá trị của sin145° gần với giá trị nào nhất sau đây:
A. 0,57
B. 1
C. \(\frac{\sqrt{2}}{2}\)
D. 0,15
-
Câu 14:
Tính giá trị biểu thức: A = cos 0° + cos 40° + cos 120° + cos 140°
A. \(\frac{1}{2}\)
B. – 0,5
C. 1
D. 0
-
Câu 15:
Cho tam giác ABC, ta có các đẳng thức:
(I) \(sin\frac{A}{2}=\sin \frac{B+C}{2}\);
(II) \(\tan \frac{A}{2}=\cot \frac{B+C}{2}\);
(III) sinA = sin(B + C).
Có bao nhiêu đẳng thức đúng?
A. 1
B. 3
C. 2
D. 0
-
Câu 16:
Cho điểm M(x0; y0) nằm trên đường tròn đơn vị thỏa mãn \(\widehat {xOM} = \alpha \). Khi đó phát biểu nào dưới đây là sai?
A. sinα = x0;
B. cosα = x0;
C. tanα = \(\frac{{{y_0}}}{{{x_0}}}\);
D. cotα = \(\frac{{{y_0}}}{{{x_0}}}\).
-
Câu 17:
Trong các công thức dưới đây, công thức nào sai về cách tính diện tích tam giác ABC? Biết AB = c, AC = b, BC = a, ha, hb, hc lần lượt là các đường cao kẻ từ đỉnh A, B, C, r là bán kính đường tròn nội tiếp, R là bán kính đường tròn ngoại tiếp tam giác ABC.
A. SABC = pr;
B. SABC = \(\frac{1}{2}\)c.a.sinA;
C. SABC = \(\sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \);
D. SABC = \(\frac{{abc}}{{4R}}\).
-
Câu 18:
Cho tam giác ABC, có các cạnh AB = c, AC = b, BC = a. Định lí sin được phát biểu:
A. \(\frac{a}{{{\rm{cos}}A}} = \frac{b}{{\cos B}} = \frac{c}{{\cos C}}\)
B. \(\frac{a}{{{\rm{sin}}A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}}\)
C. a.cosA = b.cosB = c.cosC
D. a.sinA = b.sinB = c.sinC
-
Câu 19:
Cho tam giác ABC có BC = 50 cm, \(\hat B = 65^\circ ,\hat C = 45^\circ \). Tính (làm tròn kết quả đến hàng phần mười theo đơn vị xăng – ti – mét). Chu vi của tam giác ABC là:
A. 135,84;
B. 67,92;
C. 131,91;
D. 65,96.
-
Câu 20:
Một người đứng ở vị trí A trên nóc một ngôi nhà cao 8m đang quan sát một cây cao cách ngôi nhà 25m và đo được \(\widehat {BAC} = 65^\circ \). Chiều cao của cây gần với kết quả nào nhất sau đây?
A. 38m;
B. 39m;
C. 19m;
D. 20m.
-
Câu 21:
Đẳng thức nào sau đây, mô tả đúng hình vẽ bên?

A. \(3\overrightarrow {AI} + \overrightarrow {AB} = \vec 0\)
B. \(\overrightarrow {BI} + 3\overrightarrow {BA} = \vec 0\)
C. \(3\overrightarrow {IA} + \overrightarrow {IB} = \vec 0\)
D. \(\overrightarrow {AI} + 3\overrightarrow {AB} = \vec 0\)
-
Câu 22:
Cho hình chữ nhật ABCD. Hãy chọn khẳng định đúng.
A. \(\overrightarrow{AB}=\overrightarrow{AD}\)
B. \(\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}\)
C. \(\left| \overrightarrow{AB} \right|=\left| \overrightarrow{AD} \right|\)
D. \(\overrightarrow{AB}=\overrightarrow{CD}\)
-
Câu 23:
Cho hình bình hành ABCD với điểm K thỏa mãn \(\overrightarrow{KA}+\overrightarrow{KC}=\overrightarrow{AB}\) thì
A. K là trung điểm của AC.
B. K là trung điểm của AD.
C. K là trung điểm của AB.
D. K là trung điểm của BD.
-
Câu 24:
Cho tam giác đều ABC có AB = a, M là trung điểm của BC. Khi đó \(\left| \overrightarrow{MA}+\overrightarrow{AC} \right|\) bằng
A. \(\frac{a}{4}\).
B. 2a.
C. \(\frac{a}{2}\).
D. a.
-
Câu 25:
Cho hình bình hành ABCD. Mệnh đề nào sau đây đúng?
A. \(\overrightarrow{AC}=\overrightarrow{BC}\)
B. \(\overrightarrow{AD}=\overrightarrow{CD}\)
C. \(\overrightarrow{AB}=\overrightarrow{DC}\)
D. \(\overrightarrow{AC}=\overrightarrow{BD}\)
-
Câu 26:
Cho hình chữ nhật ABCD tâm O. Gọi M, N lần lượt là trung điểm của các cạnh AB, AD. Chọn khẳng định đúng trong các khẳng định sau:
A. \(\overrightarrow{AB}=\overrightarrow{CD}\)
B. \(\overrightarrow{AN}=\overrightarrow{MO}\)
C. \(\overrightarrow{OC}=\overrightarrow{OD}\)
D. \(\overrightarrow{AM}=\overrightarrow{BM}\)
-
Câu 27:
Phát biểu nào sau đây là sai?
A. Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó.
B. Vectơ là đoạn thẳng có hướng.
C. Hai vectơ cùng hướng thì cùng phương.
D. Hai vectơ cùng phương thì cùng hướng.
-
Câu 28:
Cho hình thang MNPQ, MN // PQ, MN = 2PQ. Phát biểu nào dưới đây là đúng?
A. \(\overrightarrow{MN}=2\overrightarrow{PQ}\)
B. \(\overrightarrow{MQ}=2\overrightarrow{NP}\)
C. \(\overrightarrow{MN}=-2\overrightarrow{PQ}\)
D. \(\overrightarrow{MQ}=-2\overrightarrow{NP}\)
-
Câu 29:
Cho tam giác đều ABC nội tiếp đường tròn tâm O bán kính bằng 1. Gọi M là điểm nằm trên đường tròn (O), độ dài vectơ \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} \) bằng
A. 1
B. 6
C. \(\sqrt 3 \)
D. 3
-
Câu 30:
Cho tam giác ABC đều có cạnh bằng a, gọi H là trung điểm của cạnh BC. Độ dài của vectơ \(2\left( {\overrightarrow {HA} - \overrightarrow {HC} } \right)\) bằng
A. a
B. 2a
C. \(\frac{{a\sqrt 3 }}{2}\)
D. \(a\sqrt 3 \)
-
Câu 31:
Kí hiệu nào sau đây để chỉ \(\sqrt 5 \) không phải là số hữu tỉ?
A. \(\sqrt 5 \ne Q\)
B. \(\sqrt 5 \not\subset Q\)
C. \(\sqrt 5 \notin Q\)
D. \(\sqrt 5 \in Q\)
-
Câu 32:
Một nhóm các học sinh lớp 10H giỏi Toán hoặc giỏi Văn. Trong đó, có 5 bạn giỏi Toán; 7 bạn giỏi Văn và 2 bạn giỏi cả hai môn. Hỏi nhóm đó có bao nhiêu học sinh?
A. 14
B. 10
C. 12
D. 7
-
Câu 33:
Cho tập A = (−∞; 1] và B = (m; +∞). Tất cả các giá trị của m để A ∩ B ≠ ∅ là:
A. m > 1;
B. m ≤ 1;
C. m < 1;
D. m ≥ 1.
-
Câu 34:
Cho A = (−20; 20) và B = [2m – 4; 2m + 2) (m là tham số). Có tất cả bao nhiêu giá trị nguyên dương của tham số m để B ⊂ A?
A. 9;
B. 17
C. 8
D. 10
-
Câu 35:
Cho hai tập hợp A = [−1; 3), B = [a; a + 3]. Với giá trị nào của a thì A ∩ B = \(\emptyset \)?
A. \(\left[ {\begin{array}{*{20}{l}} {a \ge 3}\\ {a \le - 4} \end{array}} \right.\)
B. \(\left[ {\begin{array}{*{20}{l}} {a > 3}\\ {a < - 4} \end{array}} \right.\)
C. \(\left[ {\begin{array}{*{20}{l}} {a \ge 3}\\ {a < - 4} \end{array}} \right.\)
D. \(\left[ {\begin{array}{*{20}{l}} {a > 3}\\ {a \le - 4} \end{array}} \right.\)
-
Câu 36:
Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình: 2x + y < 1?
A. (0; 0);
B. (3; – 7);
C. (– 2; 1);
D. (0; 1).
-
Câu 37:
Cặp số (2; 3) là nghiệm của bất phương trình nào sau đây?
A. 2x – 3y – 1 > 0;
B. x – y < 0;
C. 4x – 3y > 0;
D. x – 3y + 7 < 0.
-
Câu 38:
Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}
2x - 5y - 1 > 0\\
2x + y + 5 > 0\\
x + y + 1 < 0
\end{array} \right.\) ?A. (0; 0);
B. (1; 0);
C. (0; – 2);
D. (0; 2).
-
Câu 39:
Phần nửa mặt phẳng tô đậm (không kể đường thẳng d) là miền nghiệm của bất phương trình nào?

A. x – y > – 2;
B. x – y > 2;
C. x – y < – 2;
D. x + y < 2.
-
Câu 40:
Phần nửa mặt phẳng không bị gạch (kể cả đường thẳng d) trong hình dưới đây là miền nghiệm của bất phương trình nào?
.png)
A. x + 2y ≥ – 2;
B. 2x + y ≤ 2;
C. 2x + y ≥ – 2;
D. x + 2y ≥ 2.











