Đề thi giữa HK1 môn Toán 10 CTST năm 2022-2023
Trường THPT Bùi Thị Xuân
-
Câu 1:
Trong các bất phương trình dưới đây, bất phương trình nào là bất phương trình bậc nhất hai ẩn?
A. 0x + 7y > 9 + 7y;
B. \(\frac{1}{x}+y\le -10\);
C. x2 – 2y < 0;
D. \(\frac{1}{2}\)x + 0.y2 ≥ 5 – y.
-
Câu 2:
Cho A=(−∞;5], B=(0;+∞). Tập hợp A∩B là:
A. [0; 5].
B. R
C. (0; 5);
D. (0; 5].
-
Câu 3:
Cho tam giác ABC có sinA = \(\frac{\sqrt{3}}{2}\). Tính sin(B + C).
A. sin(B + C) = \(\frac{\sqrt{3}}{2}\)
B. sin(B + C) = \(\frac{1}{2}\)
C. sin(B + C) = \(-\frac{\sqrt{3}}{2}\)
D. sin(B + C) = \(-\frac{1}{2}\)
-
Câu 4:
Tính giá trị biểu thức sau: M = sin75° + tan45° + cos165°.
A. M = 1;
B. M = 2;
C. M = 0;
D. M = – 1.
-
Câu 5:
Cho hình thoi ABCD có góc \(\widehat{DAB}=60{}^\circ \) cạnh 2a. Gọi O là giao điểm của hai đường chéo. Mệnh đề nào sau đây sai?
A. \(\left| \overrightarrow{AD}+\overrightarrow{AB} \right|=2a\sqrt{3}\)
B. \(\left| \overrightarrow{OB}+\overrightarrow{AD} \right|=a\frac{\sqrt{3}}{2}\)
C. \(\left| \overrightarrow{OB}-\overrightarrow{DC} \right|=a\sqrt{3}\)
D. \(\left| \overrightarrow{BA}-\overrightarrow{BC} \right|=2a\sqrt{3}\)
-
Câu 6:
Cho tam giác ABC với M là trung điểm của BC. Mệnh đề nào sau đây là đúng?
A. \(\overrightarrow{AM}+\overrightarrow{MB}+\overrightarrow{AB}=\vec{0}\)
B. \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\vec{0}\)
C. \(\overrightarrow{AM}+\overrightarrow{MC}+\overrightarrow{CA}=\vec{0}\)
D. \(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AM}=\vec{0}\)
-
Câu 7:
Cho hình bình hành ABCD, có AB = 4, BC = 5, BD = 7. Độ dài của AC gần nhất với giá trị nào sau đây:
A. 7,0
B. 5,9
C. 5,7
D. 7,5
-
Câu 8:
Cho hình bình hành ABCD . Mệnh đề nào sau đây là đúng?
A. \(\overrightarrow{AC}+\overrightarrow{CD}=\overrightarrow{BC}\)
B. \(\overrightarrow{BA}+\overrightarrow{BC}=\overrightarrow{AC}\)
C. \(\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{BD}\)
D. \(\overrightarrow{CA}+\overrightarrow{AD}=\overrightarrow{DC}\)
-
Câu 9:
Cho tập M = {1; 2; 3; 4; 5} và tập N = {3; 4; 5}. Số các tập X có 4 phần tử thỏa mãn N ⊂ X ⊂ M là:
A. 1
B. 2
C. 3
D. 4
-
Câu 10:
Cho tam giác ABC có AB = 6, \(\hat{C}=45{}^\circ ,\hat{A}=80{}^\circ \). Độ dài cạnh BC là:
A. BC ≈ 8,4;
B. BC ≈ 4,3;
C. BC ≈ 7,0;
D. BC ≈ 5,2.
-
Câu 11:
Gọi D là tập xác định của hàm số \(y=\frac{\sqrt{x+2}}{{{x}^{2}}+x-12}\). Tìm tập hợp R\D:
A. R\D = [– 2; +∞) \ {3};
B. R\D = (– ∞; – 2);
C. R\D = (– ∞; – 2) \ {– 4};
D. R\D = [– 2; +∞) \ {– 4}.
-
Câu 12:
Trong các câu sau, câu nào không phải là mệnh đề ?
A. Hôm nay trời mưa to quá!;
B. Hà Nội là thủ đô của nước Việt Nam;
C. \(\sqrt{5}\) là số vô tỉ;
D. 6 là số nguyên tố.
-
Câu 13:
Cặp số nào sau đây không là nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}
{x + y \le 2}\\
{2x - 3y > - 2}
\end{array}} \right..\)A. (0; 0)
B. (1; 1)
C. (– 1; 1)
D. (– 1; – 1)
-
Câu 14:
Cho tam giác đều ABC có cạnh bằng 1. Giá trị \(\left| \overrightarrow{AB}-\overrightarrow{CA} \right|\) bằng bao nhiêu?
A. \(2\sqrt{3}\)
B. \(\frac{\sqrt{3}}{2}\)
C. \(\sqrt{3}\)
D. \(4\sqrt{3}\)
-
Câu 15:
Cho A = {x ∈ N| x chia hết cho 3 và x chia hết cho 2}, B = {x ∈ N| x chia hết cho 12}. Nhận xét nào dưới đây là đúng?
A. A ⊂ B;
B. B ⊂ A;
C. A = B;
D. Các đáp án A, B, C đều sai.
-
Câu 16:
Miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}
x + 2y < 2\\
x \ge 0\\
y \ge 0
\end{array} \right.\) là:A. miền trong tam giác OAB với A(2; 0), B(0; 1) và O (0; 0);
B. miền trong tứ giác OMNP với O(0; 0), M(2; 0), N(0; 1) và P(– 2; 2);
C. nửa mặt phẳng giới hạn bởi các đường thẳng Ox, Oy và đường thẳng x + 2y = 2;
D. nửa mặt phẳng bờ là đường thẳng x + 2y = 2 không chứa gốc tọa độ O(0; 0).
-
Câu 17:
Với tam giác ABC có bao nhiêu vectơ khác vectơ - không có điểm đầu và điểm cuối là ba đỉnh của tam giác?
A. 6
B. 4
C. 5
D. 3
-
Câu 18:
Các phần tử của tập hợp A = {x ∈ R: 2x2 – 5x – 7 = 0} là:
A. \(A = \left\{ { - 1;\frac{3}{2}} \right\}\)
B. \(A = \left\{ { - 1} \right\}\)
C. \(A = \left\{ { - 1;\frac{7}{2}} \right\}\)
D. \(A = \left\{ {\frac{7}{2}} \right\}\)
-
Câu 19:
Cho các điểm phân biệt A, B, C, D. Đẳng thức nào sau đây đúng ?
A. \(\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{BA}\)
B. \(\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{CA}\)
C. \(\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\)
D. \(\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{CB}\)
-
Câu 20:
Cho tam giác ABC có BC = 24, AC = 13, AB = 15. Nhận xét nào sau đây đúng về tam giác ABC.
A. ABC là tam giác tù, với \(\hat A \approx 150^\circ \)
B. ABC là tam giác vuông tại A
C. ABC là tam giác nhọn
D. ABC là tam giác tù, với \(\hat A \approx 118^\circ \)
-
Câu 21:
Xét mệnh đề P: “∃ x ∈ R: 2x – 3 ≥ 0”. Mệnh đề phủ định \(\overline{\text{P}}\) của mệnh đề P là
A. “∃ x ∈ R: 2x – 3 ≥ 0”
B. “∀ x ∈ R: 2x – 3 < 0”
C. “∀ x ∈ R: 2x – 3 ≤ 0”
D. “∃ x ∈ R: 2x – 3 > 0”
-
Câu 22:
Trong các mệnh đề sau, mệnh đề nào đúng?
A. Để tứ giác T là một hình vuông, điều kiện cần và đủ là nó có 4 cạnh bằng nhau
B. Để tổng hai số tự nhiên chia hết cho 7, điều kiện cần và đủ là mỗi số đó chia hết cho 7
C. Để ab > 0, điều kiện cần là cả hai số a và b đều dương
D. Để một số nguyên dương chia hết cho 3, điều kiện đủ là nó chia hết cho 9
-
Câu 23:
Mệnh đề chứa biến: “\({x^3} - 3{x^2} + 2x = 0\)” đúng với giá trị nào của x?
A. x ∈ {0; 2};
B. x ∈ {0; 3};
C. x ∈ {0; 2; 3};
D. x ∈ {0; 1; 2}.
-
Câu 24:
“Nếu a và b là hai số hữu tỉ thì tổng a + b cũng là số hữu tỉ”. Cách phát biểu nào sau đây diễn đạt mệnh đề trên?
A. Điều kiện cần để tổng a + b là số hữu tỉ là cả hai số a và b đều là số hữu tỉ;
B. Điều kiện đủ để tổng a + b là số hữu tỉ là cả hai số a và b đều là số hữu tỉ;
C. Điều kiện cần và đủ để cả hai số a và b hữu tỉ là tổng a + b là số hữu tỉ;
D. Tất cả các câu đều sai.
-
Câu 25:
Trong các tập hợp sau đây, tập hợp nào có đúng hai tập con:
A. {x; y};
B. {x};
C. {\(\emptyset \); x};
D. {\(\emptyset \); y}.
-
Câu 26:
Cho 3 tập hợp E, F, G sao cho E ⊂ F, F ⊂ G và G ⊂ E. Câu nào sau đây đúng?
A. G ⊂ F;
B. E ⊂ G;
C. E = G;
D. E = F = G.
-
Câu 27:
Lớp 10A của trường có 20 học sinh thích môn Toán, 18 học sinh thích môn Ngữ văn và 10 học sinh thích cả môn Toán và Ngữ văn. Hỏi lớp 10A có bao nhiêu học sinh thích ít nhất 1 trong 2 môn Toán và môn Ngữ văn?
A. 28
B. 38
C. 20
D. 2
-
Câu 28:
Cho hai tập hợp A ={1;2;3;7;9}và B ={1;2;7;10}. Tập hợp A ∪ Bcó bao nhiêu phần tử?
A. 4
B. 3
C. 5
D. 6
-
Câu 29:
Cho A = {0; 1; 2; 3; 4} và B = {2; 3; 4; 5; 6}. Tập hợp (A\B) ∩ (B\A) bằng:
A. {5};
B. {0; 1; 5; 6};
C. {1; 2};
D. \(\emptyset \) .
-
Câu 30:
Cho các tập hợp A, B, C được minh hoạ bằng biểu đồ Ven như hình vẽ dưới đây:
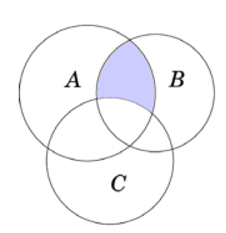
Phần tô màu xám trong hình vẽ biểu diễn của tập hợp nào sau đây?
A. A ∩ B ∩ C;
B. (A\B) ∪ (A\C);
C. (A ∪ B) \ C;
D. (A ∩ B) \ C.
-
Câu 31:
Trong các bất phương trình sau đây, đâu là bất phương trình bậc nhất hai ẩn?
A. 3x + 4y – z + 1 > 0;
B. 2x – 2y – 1 > 0;
C. x2 + y < 3;
D. \(\frac{{3x}}{{4y}}\) - x > 0.
-
Câu 32:
Cặp số nào sau đây là nghiệm của bất phương trình bậc nhất hai ẩn: 2x + y – 1 < 0?
A. (x; y) = (2; 3);
B. (x; y) = (1; 2);
C. (x; y) = (0; 1);
D. (x; y) = (-1; 0).
-
Câu 33:
Hình vẽ sau biểu diễn miền nghiệm (phần không bị gạch) của bất phương trình bậc nhất hai ẩn nào?
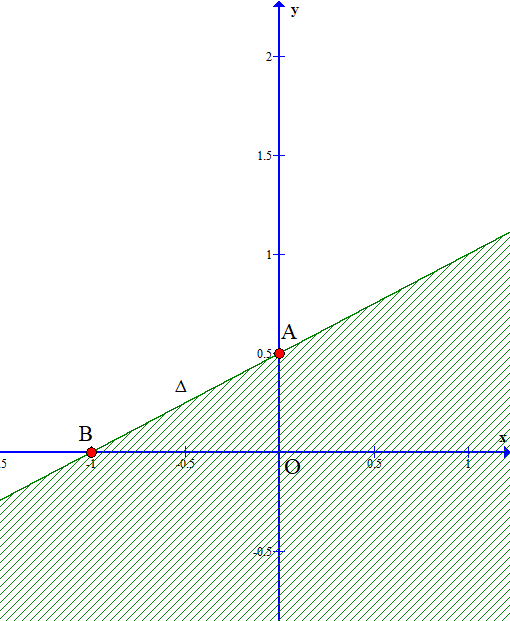
A. x + 2y – 2 > 0
B. 3x + y – 2 < 0
C. x – 2y + 1 < 0
D. x + 3y > 0
-
Câu 34:
Cho bất phương trình x - 3y – 1 ≤ 0. Chọn khẳng định đúng trong các khẳng định sau:
A. Bất phương trình đã cho chỉ có một nghiệm duy nhất;
B. Bất phương trình đã cho vô nghiệm;
C. Bất phương trình đã cho luôn có vô số nghiệm;
D. Bất phương trình đã cho có tập nghiệm là R.
-
Câu 35:
Điểm nào sau đây thuộc miền nghiệm của bất phương trình bậc nhất hai ẩn x + 2y – 1 > 0 trên mặt phẳng tọa độ Oxy?
A. A(- 4; - 5);
B. B(2; 3);
C. C(- 2; -1);
D. D(0; -2).
-
Câu 36:
Cho α là góc tù. Khẳng định nào sau đây là đúng?
A. sin α < 0;
B. cos α > 0;
C. tan α < 0;
D. cot α > 0.
-
Câu 37:
Cho hai góc α và β (0° ≤ α, β ≤ 180°) với α + β = 90°. Giá trị của biểu thức P = cosα.cosβ ‒ sinα.sinβ là:
A. P = 0;
B. P = 1;
C. P = ‒ 1;
D. P = 2.
-
Câu 38:
Trong các đẳng thức sau, đẳng thức nào đúng?
A. sin(180° – α) = ‒cos α;
B. sin(180° – α) = ‒sin α;
C. sin(180° – α) = sin α;
D. sin(180° – α) = cos α.
-
Câu 39:
Tam giác ABC có \(BC = 5\sqrt 5 ,AC = 5\sqrt 2 ,AB = 5\). Số đo góc \(\widehat A\) là:
A. 30°
B. 45°
C. 120°
D. 135°
-
Câu 40:
Tam giác ABC có ba cạnh lần lượt là: 2, 3, 4. Góc nhỏ nhất của tam giác có côsin bằng bao nhiêu?
A. \(\frac{{\sqrt {15} }}{8}\)
B. \(\frac{7}{8}\)
C. \(\frac{1}{2}\)
D. \(\frac{{\sqrt {14} }}{8}\)











