Đề thi giữa HK1 môn Toán 10 năm 2020
Trường THPT Nguyễn Hiền
-
Câu 1:
Cho mệnh đề chứa biến P: “x+1 < 4”. Tìm x để được mệnh đề đúng.
A. x = 2
B. x = 3
C. x = 4
D. x = 5
-
Câu 2:
Mệnh đề nào sau đây là sai
A. 30 chia hết cho 6
B. 9 + 1 =10
C. 2 < \(\sqrt4\)
D. \(\frac{1}{2} + \frac{1}{3} = \frac{5}{6}\)
-
Câu 3:
Phủ định của mệnh đề P: “9 chia hết cho 3” là
A. 3 chia hết 9
B. 9 không chia hết cho 3
C. 9 là bội số của 3
D. 3 không chia hết cho 9
-
Câu 4:
Trong các mệnh đề sau, mệnh đề nào đúng?
A. Để tứ giác là một hình vuông, điều kiện cần và đủ là nó có bốn cạnh bằng nhau
B. Để tổng hai số tự nhiên chia hết cho 7, điều kiện cần và đủ là mỗi số đó chia hết cho 7
C. Để cả 2 số a và b đều dương, điều kiện cần là ab > 0
D. Để một số nguyên chia hết cho 3, điều kiện đủ là nó chia hết cho 9
-
Câu 5:
Cho mệnh đề “Nếu tứ giác là một hình thoi thì tứ giác đó nội tiếp được một đường tròn”. Mệnh đề nào sau đây tương đương với mệnh đề đã cho
A. Điều kiện đủ để tứ giác là hình thoi là tứ giác đó nội tiếp được một đường tròn
B. Điều kiện đủ để tứ giác nội tiếp được một đường tròn là tứ giác đó là hình thoi
C. Điều kiện đủ để tứ giác là hình thang cân là tứ giác có hai đường chéo bằng nhau
D. Cả A, B đều đúng
-
Câu 6:
Cho mệnh đề “Nếu tứ giác là một hình thoi thì tứ giác đó nội tiếp được một đường tròn”. Mệnh đề nào sau đây tương đương với mệnh đề đã cho
A. Điều kiện đủ để tứ giác là hình thoi là tứ giác đó nội tiếp được một đường tròn
B. Điều kiện đủ để tứ giác nội tiếp được một đường tròn là tứ giác đó là hình thoi
C. Điều kiện đủ để tứ giác là hình thang cân là tứ giác có hai đường chéo bằng nhau
D. Cả A, B đều đúng
-
Câu 7:
Tập \(S = \left\{ {q \in Q|25{q^4} - 9{q^2} = 0} \right\}\) có bao nhiêu phần tử.
A. 4
B. 1
C. 2
D. 3
-
Câu 8:
Chọn khẳng định đúng:
A. \(\left\{ 1 \right\} \subset \left[ {1;\frac{5}{2}} \right]\)
B. \( - 2 \in \left( { - 2;6} \right)\)
C. \(1 \notin \left[ {1;\frac{5}{2}} \right]\)
D. \(4 \subset \left[ {3;5} \right]\)
-
Câu 9:
Cho A là tập hợp gồm các số tự nhiên lẻ nhỏ hơn 14, B là tập hợp gồm các số nguyên tố nhỏ hơn 10. Vậy \(A \cap B\) là
A. {2; 3; 5; 7}
B. {5; 7}
C. {1; 3; 5; 7}
D. {3; 5; 7}
-
Câu 10:
Cho A là tập hợp gồm các số tự nhiên lẻ nhỏ hơn 14, B là tập hợp gồm các số nguyên tố nhỏ hơn 10. Vậy \(A \cap B\) là
A. {2; 3; 5; 7}
B. {5; 7}
C. {1; 3; 5; 7}
D. {3; 5; 7}
-
Câu 11:
Mỗi học sinh của lớp 10A1 đều biết chơi đá cầu hoặc cầu lông, biết rằng có 25 em biết chơi đá cầu, 30 em biết chơi cầu lông, 15 em biết chơi cả hai . Hỏi lớp 10A1 có bao nhiêu em?
A. 10
B. 40
C. 15
D. 25
-
Câu 12:
Cho tập hợp A = {0;1;2;3;4} và B = {0;2;4;6;8}. Hỏi tập hợp (A∖B) ∪ (B∖A) có bao nhiêu phần tử?
A. 7
B. 4
C. 10
D. 3
-
Câu 13:
Cho tập hợp A. Tìm mệnh đề SAI trong các mệnh đề sau ?
A. A ∩ ∅ = ∅.
B. ∅ ⊂ A
C. A ∈ {A}
D. A ∈ {A}
-
Câu 14:
Cho tập hợp A = {x ∈ R| 2 ≤ x < 5}. Xác định phần bù của tập hợp A trong R.
A. [5; +∞)
B. (−∞; 2) ∪ [5; +∞)
C. (−∞; 2)
D. (−∞; 2] ∪ (5; +∞)
-
Câu 15:
Trong các tập sau đây, tập nào là tập con của tập nào
A = {1; 2; 3}
B = {n ∈ N |n < 4}
C = (0; +∞)
D = {x ∈ R ∣2x 2 − 7x + 3 = 0}
A. A ⊂ B
B. C ⊂ A
C. C ⊂ D
D. Cả A, B, C đều đúng
-
Câu 16:
Xác định các tập số sau: (−4; 2] ∩ [0; 4)
A. [0; 2]
B. (-4; 4)
C. [2; 4)
D. [-4; 4)
-
Câu 17:
Tìm m để (1; m] ∩ (2; +∞) ≠ ∅
A. m < 2
B. m > 2
C. m ≤ 2
D. m ≥ 2
-
Câu 18:
Viết tập A gồm các phần tử x thỏa mãn điều kiện \(\left\{ \begin{array}{l} x \le 3\\ x + 1 \ge 0\\ x < 0 \end{array} \right.\) dưới dạng tập số
A. A = [0; 1)
B. A = [-1; 0)
C. A = [-1; 1)
D. A = [1; 0)
-
Câu 19:
Cho các tập hợp A = (−∞; m) và B = [3m − 1; 3m + 3]. Tìm m để CRA ∩ B ≠ ∅
A. m > -1,5
B. m ≤ -1,5
C. m ≥ -1,5
D. m < -1,5
-
Câu 20:
Hàm số nào dưới đây đồng biến trên tập R?
A. y = −2 + 3x
B. \(y=\frac2x\)
C. \(y=\sqrt{x+3}\)
D. y = -x +2
-
Câu 21:
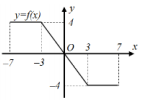
Cho hàm số y = f(x) xác định trên các đoạn [-7 ; 7], đồ thị của nó là các đoạn thẳng được biểu diễn bởi hình bên. Khẳng định nào sau đây sai?
A. Hàm số nghịch biến trên khoảng (-7 ; 7)
B. Hàm số đại giá trị nhỏ nhất trên khoảng (−7; 7) là -4
C. Hàm số là hàm hằng trên đoạn [-7; -3]
D. \(f(x) = - \frac{4}{3}x,\forall x \in \left[ { - 3;3} \right]\)
-
Câu 22:
Cho hàm số f(x) = |-5x|. Khẳng định nào sau đây sai?
A. f(2) = 10
B. f(-1) = 5
C. f(-2) = 10
D. \(f(\frac15)=-1\)
-
Câu 23:
Cho hàm số y = f (x) = |x + 2018| + |x − 2018|. Chọn mệnh đề sai trong các mệnh đề sau:
A. Đồ thị hàm số y = f(x) nhận gốc tọa độ O làm tâm đối xứng.
B. Hàm số y = f(x) là hàm số chẵn
C. Đồ thị hàm số y = f(x) nhận trục tung làm trục đối xứng
D. Có tập xác định là R
-
Câu 24:
Cho hàm số y = f(x) = 4 -3x. Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên \(\left( { - \infty ;\frac{4}{3}} \right)\)
B. Hàm số nghịch biến trên \(\left( {\frac{4}{3}; + \infty } \right)\)
C. Hàm số nghịch biến trên R
D. Hàm số đồng biến trên \(\left( {\frac{3}{4}; + \infty } \right)\)
-
Câu 25:
Cho hàm số y = 2mx − m − 1 (d). Tìm m để đường thẳng (d) đi qua điểm A(1; 2).
A. m < 3
B. m = - 3
C. m = 3
D. Không tồn tại
-
Câu 26:
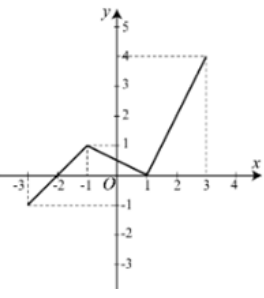
Cho hàm số y = f(x) có TXĐ là [-3; 3] và có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?
A. Đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt
B. Hàm số đồng biến trên khoảng (-3; 1) và (1; 4)
C. Hàm số nghịch biến trên khoảng (-2; 1)
D. Hàm số đồng biến trên khoảng (-3; -1) và (1; 3)
-
Câu 27:
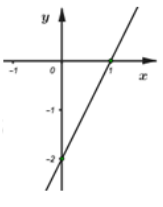
Hình vẽ sau đây là đồ thị của hàm số nào?
A. y = x - 2
B. y = -x - 2
C. y = -2x - 2
D. y = 2x - 2
-
Câu 28:
Tọa độ đỉnh của parabol (P) : y = −x 2 + 2x − 3 là:
A. (1; -2)
B. (-2; 3)
C. (-1; 2)
D. (2; -3)
-
Câu 29:
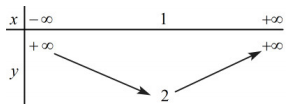
Bảng biến thiên sau là của hàm số nào?
A. y = x 2 + 2x − 1
B. y = x 2 − 2x + 2
C. y = 2x 2 − 4x + 4
D. y = −3x 2 + 6x − 1
-
Câu 30:
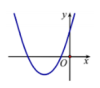
Cho hàm số y = ax 2 + bx + c có đồ thị như hình dưới đây. Mệnh đề nào sau đây đúng?
A. a > 0, b = 0, c > 0
B. a > 0, b < 0, c > 0
C. a > 0, b > 0, c > 0
D. a < 0, b > 0, c > 0