Đề thi giữa HK2 môn Toán 7 năm 2021
Trường THCS Vĩnh Châu
-
Câu 1:
Mệnh đề: “Tổng các bình phương của ba số a, b và c” được biểu thị bởi
A. \( {\left( {a + b + c} \right)^2}\)
B. \( {\left( {a + b } \right)^2}+c\)
C. \( a^2+b^2+c^2\)
D. \( a^3+b^3+c^3\)
-
Câu 2:
Mệnh đề: “Tổng các lập phương của hai số a và b” được biểu thị bởi
A. \( {a^3} + {b^3}\)
B. \((a+b)^3\)
C. \( {a^2} + {b^2}\)
D. \((a+b)^2\)
-
Câu 3:
Viết biểu thức đại số biểu thị “Nửa tổng của hai số c và d”.
A. \(c+d\)
B. \(\frac{1}{2}\left( {c +d} \right)\)
C. \(\frac{1}{2};c;d\)
D. \(\frac{1}{2}\left( {c - d} \right)\)
-
Câu 4:
Viết biểu thức đại số biểu thị “Nửa hiệu của hai số a và b”
A. a−b
B. a.b
C. 1/2(a−b)
D. a+b
-
Câu 5:
Cho m,n là các hằng số. Tìm các biến trong biểu thức đại số \(2mz + n(z + t) \)
A. m;z;n;t
B. z;n
C. z;t
D. m;z;t
-
Câu 6:
Cho a,b là các hằng số. Tìm các biến trong biểu thức đại số \(x(a^2- ab + b^2 ) + y\)
A. a;b
B. a;b;x;y
C. a;b;x
D. x;y
-
Câu 7:
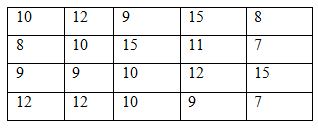
Số lượng học sinh nữ của một lớp trong một trường Trung học cơ sở được ghi nhận trong bảng sau.
.png)
Có bao giá trị khác nhau của dấu hiệu?
A. 7 giá trị
B. 9 giá trị
C. 14 giá trị
D. 20 giá trị
-
Câu 8:
Số lượng học sinh giỏi trong từng lớp của một trường trung học cơ sở được ghi lại bởi bảng dưới đây
Dấu hiệu cần tìm hiểu ở đây là gì?
A. Số học sinh trong mỗi lớp
B. Số học sinh khá của mỗi lớp
C. Số học sinh giỏi trong mỗi lớp
D. Số học sinh giỏi trong mỗi trường
-
Câu 9:
Kết quả môn nhảy cao (tính bằng cm) của học sinh lớp 7A được ghi lại trong bảng sau:
Có bao nhiêu học sinh tham gia kiểm tra?
A. 30
B. 34
C. 28
D. 32
-
Câu 10:
Thời gian giải một bài toán (tính theo phút) của học sinh lớp 7 được ghi lại trong bảng sau:
Số các giá trị khác nhau của dấu hiệu là:
A. 5
B. 6
C. 7
D. 8
-
Câu 11:
Tính giá trị biểu thức \(\mathrm{B}=\mathrm{x}^{2} \mathrm{y}^{2}+\mathrm{xy}+\mathrm{x}^{3}+\mathrm{y}^{3} \text { tại } \mathrm{x}=-1 ; \mathrm{y}=3\)
A. 29
B. 32
C. 38
D. 43
-
Câu 12:
Tính giá trị biểu thức \(\mathrm{A}=3 \mathrm{x}^{3} \mathrm{y}+6 \mathrm{x}^{2} \mathrm{y}^{2}+3 \mathrm{xy}^{3} \text { tại } x=\frac{1}{2} ; y=-\frac{1}{3}\)
A. \( - \frac{1}{{72}}\)
B. -25
C. \(\frac{2}{3}\)
D. \(\frac{{ - 1}}{2}\)
-
Câu 13:
Tìm giá trị lớn nhất của biểu thức \(M = 110 - (2x^2- 162 )^6\)
A. 109
B. 100
C. 110
D. 101
-
Câu 14:
Tìm giá trị lớn nhất của biểu thức \(M = 10 - (y^2- 25) ^4\)
A. 9
B. 8
C. 10
D. 11
-
Câu 15:
Biểu thức \( P = {({x^2} - 4)^2} + \left| {y - 5} \right| - 1\) đạt giá trị nhỏ nhất là
A. 2
B. 3
C. 1
D. -1
-
Câu 16:
Tìm giá trị lớn nhất của biểu thức \( B = 8 - \left| {3x - 5} \right|\)
A. 9
B. 8
C. 6
D. 0
-
Câu 17:
Bậc của đơn thức \(G=x\left[\frac{2}{9} y\left(3 x y^{2}\right)^{2}\right]^{3}\) là
A. 13
B. 19
C. 18
D. 21
-
Câu 18:
Thu gọn đơn thức \(G=x\left[\frac{2}{9} y\left(3 x y^{2}\right)^{2}\right]^{3}\) ta được
A. \(8 x^{7} y^{12}\)
B. \(-8 x^{7} y^{12}\)
C. \(8 x^{6} y^{12}\)
D. \(x^{3} y^{12}\)
-
Câu 19:
Bậc của đợn thức \(F=2 x^{3} y .\left[-3(-x) y^{4}\right]\) là
A. 3
B. 6
C. 9
D. 12
-
Câu 20:
Thu gọn đơn thức \(F=2 x^{3} y .\left[-3(-x) y^{4}\right]\) ta được
A. \(3 x^{4} y^{5}\)
B. \(6 x^{5} y^{5}\)
C. \(-6 x^{4} y^{5}\)
D. \(6 x^{4} y^{5}\)
-
Câu 21:
Bậc của đơn thức \(E=\left(-\frac{3}{5} x^{3} y^{2} z\right)^{3}\) là
A. 16
B. 17
C. 18
D. 19
-
Câu 22:
Thu gọn đơn thức \(E=\left(-\frac{3}{5} x^{3} y^{2} z\right)^{3}\) ta được
A. \(-\dfrac{27}{125} x^{9} y^{6} z^{3}\)
B. \(-\dfrac{27}{125} x^{6} y^{6} z^{3}\)
C. \(\dfrac{27}{125} x^{7} y^{6} z^{3}\)
D. \(\dfrac{27}{125} x^{9} y^{6} z^{3}\)
-
Câu 23:
Các đơn thức đồng dạng trong các đơn thức sau là: \(2 x y^{2} z, 6 x y,-3 x^{2} y,-5 x y^{2} z, 3 x y, \frac{3}{4} x^{2} y, \frac{1}{2} x y^{2} z,-\frac{1}{5} x y\)
A. \(6 x y,-3 x^{2} y,-5 x y^{2} z\)
B. \(-5 x y^{2} z, 3 x y, \frac{3}{4} x^{2} y\)
C. \(6 x y;3 x y;\frac{1}{5} x y\)
D. \(2 x y^{2} z, 6 x y,-3 x^{2} y\)
-
Câu 24:
Các đơn thức đồng dạng trong các đơn thức sau là: \(2 x y^{2} z, 6 x y,-3 x^{2} y,-5 x y^{2} z, 3 x y, \frac{3}{4} x^{2} y, \frac{1}{2} x y^{2} z,-\frac{1}{5} x y\)
A. \(2 x y^{2} z, 6 x y,-3 x^{2} y,-5 x y^{2} z\)
B. \(2 x y^{2} z;5 x y^{2} z;\frac{1}{2} x y^{2} z\)
C. \(3 x y, \frac{3}{4} x^{2} y, \frac{1}{2} x y^{2} z\)
D. \(3 x y, \frac{3}{4} x^{2} y, \frac{1}{2} x y^{2} z,-\frac{1}{5} x y\)
-
Câu 25:
Đơn thức không đồng dạng với đơn thức \(2xy^2z \) là:
A. \( - {x^3}{y^2}z\)
B. \(-xzy^2\)
C. \(3 x{y^2}z\)
D. \( \frac{1}{4}{y^2}zx\)
-
Câu 26:
Đơn thức đồng dạng với đơn thức \(3x^2y^3\) là:
A. \( - 3{x^3}{y^2}\)
B. \( - 7{x^2}{y^3}\)
C. \( \frac{1}{3}{x^5}\)
D. \( - {x^4}{y^6}\)
-
Câu 27:
Có mấy nhóm đơn thức đồng dạng với nhau trong các đơn thức sau (mỗi nhóm từ 2 đơn thức trở lên): \( 2xy;5xy;9{y^2};{y^2}\)
A. 1
B. 2
C. 3
D. 4
-
Câu 28:
Có mấy nhóm đơn thức đồng dạng với nhau (mỗi nhóm từ 2 đơn thức trở lên) trong các đơn thức sau: \( - \frac{2}{3}{x^3}y;{\mkern 1mu} 2{x^3}y;5{x^2}y;\frac{1}{2}{x^2}y; - x{y^2};6x{y^2}\)
A. 2
B. 4
C. 3
D. 5
-
Câu 29:
Độ dài hai cạnh của một tam giác là 2 cm và 10 cm. Trong các số đo sau đây, số đo nào là độ dài cạnh thứ ba của tam giác đó.
A. 6 cm
B. 7 cm
C. 8 cm
D. 9 cm
-
Câu 30:
Cho tam giác ABC có AH vuông góc với BC tại H. Khi đó ta có
A. 2AH + BC > AB + AC
B. 2AH + BC < AB + AC
C. 2AH + BC = AB + AC
D. AH + BC = AB + AC
-
Câu 31:
Cho tam giác ABC cân có AB = 3,9 cm và BC = 7,9 cm. Khi đó ta có
A. Tam giác ABC cân tại A
B. Tam giác ABC cân tại B
C. Tam giác ABC cân tại C
D. Tam giác ABC đều
-
Câu 32:
Cho tam giác ABC có BC = 1cm, AC = 8cm và độ dài cạnh AB là một số nguyên (cm). Tam giác ABC là tam giác gì?
A. Tam giác vuông tại A
B. Tam giác cân tại A
C. Tam giác vuông cân tại A
D. Tam giác cân tại B
-
Câu 33:
Cho tam giác ABC biết AB = 1cm, BC = 9cm và cạnh AC là một số nguyên. Chu vi tam giác ABC là:
A. 17cm
B. 18cm
C. 18cm
D. 16cm
-
Câu 34:
Cho ΔABC có cạnh AB = 1cm và BC = 4cm. Tính độ dài cạnh AC biết độ dài cạnh AC là một số nguyên:
A. 1cm
B. 2cm
C. 3cm
D. 4cm
-
Câu 35:
Cho tam giác ABC, trên BC lấy điểm M bất kì nằm giữa B và C. So sánh (AB + AC - BC ) và (2.AM )
A. AB+AC−BC>2.AM.
B. AB+AC−BC≥2.AM
C. AB+AC−BC=2.AM
D. AB+AC−BC<2.AM
-
Câu 36:
Có bao nhiêu tam giác có độ dài hai cạnh là 7cm và 2cm còn độ dài cạnh thứ ba là một số nguyên (đơn vị cm)?
A. 1
B. 2
C. 3
D. 4
-
Câu 37:
Cho tam giác ABC cân tại A có một cạnh bằng 5cm. Tính cạnh BC của tam giác đó biết chu vi của tam giác là 17cm.
A. BC=7cm hoặc BC=5cm.
B. BC=6cm.
C. BC=5cm
D. BC=7cm
-
Câu 38:
Cho tam giác ABC có BC = 5cm, AC = 1cm và độ dài cạnh AB là một số nguyên. Tam giác ABC là tam giác gì?
A. Tam giác vuông tại B.
B. Tam giác cân tại B
C. Tam giác vuông cân tại A
D. Tam giác cân tại A.
-
Câu 39:
Cho D là một điểm nằm trong tam giác ABC. Nếu AD = AB thì:
A. AB=AC
B. AB>AC
C. AB<AC
D. AB≤AC
-
Câu 40:
Cho tam giác ABC có 900 < góc A < 1800. Trên cạnh AB và AC lấy tương ứng hai điểm M và N (M,N không trùng với các đỉnh của am giác ABC). Chọn đáp án đúng nhất.
A. BA<BN<BC
B. BA>BN>BC
C. CA<CM<CB
D. Cả A, C đều đúng