Đề thi HK2 môn Toán 10 KNTT năm 2022-2023
Trường THPT Huỳnh Mẫn Đạt
-
Câu 1:
Phương trình tổng quát của đường thẳng đi qua hai điểm A(3 ; -1) và B(1 ; 5) là:
A. -x + 3y + 6 = 0 ;
B. 3x - y + 10 = 0 ;
C. 3x - y + 6 = 0 ;
D. 3x + y - 8 = 0.
-
Câu 2:
Phương trình đường thẳng cắt hai trục tọa độ tại A(-2 ; 0) và B(0 ; 3) là:
A. 2x - 3y + 4 = 0 ;
B. 3x - 2y + 6 = 0 ;
C. 3x - 2y - 6 = 0 ;
D. 2x - 3y - 4 = 0.
-
Câu 3:
Xét vị trí tương đối của hai đường thẳng:
d1: x – 2y + 1 = 0 và d2: – 3x + 6y – 10 = 0
A. Trùng nhau.
B. Song song.
C. Vuông góc với nhau.
D. Cắt nhau nhưng không vuông góc nhau.
-
Câu 4:
Tọa độ tâm I và bán kính R của đường tròn \((C):(x−1)^2+(y+3)^2=16\) là:
A. I (-1; 3), R = 4;
B. I (1; -3), R = 4;
C. I (1; -3), R = 16
D. I (-1; 3), R = 16.
-
Câu 5:
Đường tròn \((C): x^2 + y^2 – 6x + 2y + 6 = 0\) có tâm I và bán kính R lần lượt là:
A. I(3; −1) và R = 4;
B. I(3; 1) và R = 4;
C. I(3; −1) và R = 2;
D. I(-6; 2) và R = 2.
-
Câu 6:
Cho parabol (P) có phương trình chính tắc là \({y^2} = 2px\), với p > 0. Khi đó khẳng định nào sau đây sai?
A. Tọa độ tiêu điểm F(p/2;0);
B. Phương trình đường chuẩn Δ:x+p/2=0;
C. Trục đối xứng của parabol là trục Oy.
D. Parabol nằm về bên phải trục Oy.
-
Câu 7:
Biểu thức nào sau đây là tam thức bậc hai
A. \(f(x) = x + 2\);
B. \(f(x) = 2x ^3 + 2x2 – 1\);
C. \(f(x) = x^2 – 3x\);
D. \(f(x) = 2x – 1\).
-
Câu 8:
Các giá trị m làm cho biểu thức \(f(x) = x^2 + 4x + m + 3\) luôn dương là
A. m < 1;
B. m ≥ 1;
C. m > 1;
D. m∈∅.
-
Câu 9:
Tập nghiệm của bất phương trình \(x^2\) – x – 6 ≤ 0 là:
A. (–∞; – 3]∪[2; + ∞);
B. [– 3; 2];
C. [– 2; 3];
D. (– ∞; – 2]∪[3; + ∞) ;
-
Câu 10:
Phương trình:\(\sqrt { - {x^2} + 6x - 5} = 8 - 2x\) có nghiệm là:
A. x = 3 ;
B. x = 23/5;
C. x = 3 hoặc x = 23/5 ;
D. x = – 3.
-
Câu 11:
Cho các chữ số 2, 3, 4, 5, 6, 7 số các số tự nhiên chẵn có 3 chữ số lập thành từ các chữ số đã cho là:
A. 36;
B. 18;
C. 256;
D. 108;
-
Câu 12:
Bạn Dũng có 8 quyển truyện tranh khác nhau và 7 quyển tiểu thuyết khác nhau. Bạn Dũng có bao nhiêu cách chọn ra một quyển sách để đọc vào cuối tuần.
A. 8;
B. 7;
C. 56;
D. 15.
-
Câu 13:
Tên 15 học sinh được ghi vào 15 tờ giấy để vào trong hộp. Có bao nhiêu cách chọn tên 4 học sinh để cho đi du lịch
A. 4!;
B. 15!.
C. 1365;
D. 32760.
-
Câu 14:
Trong khai triển nhị thức \((a + 2)^{n + 6}\) (n ∈ ℕ). Có tất cả 17 số hạng. Vậy n bằng
A. 17;
B. 11;
C. 10;
D. 12.
-
Câu 15:
Gieo một đồng tiền liên tiếp 3 lần thì số phần tử của không gian mẫu n(Ω) là
A. 4
B. 6
C. 8
D. 16
-
Câu 16:
Gieo một con xúc xắc cân đối đồng chất 2 lần. Số phần tử của không gian mẫu là?
A. 6;
B. 12;
C. 18;
D. 36.
-
Câu 17:
Cho A là một biến cố liên quan đến phép thử T. Mệnh đề nào sau đây là mệnh đề đúng?
A. P(A) là số lớn hơn 0;
B. P(A) = 1 – P(\(\overline A \));
C. P(A) = 0 ⇔ A = Ω;
D. P(A) là số nhỏ hơn 1.
-
Câu 18:
Một lớp có 20 học sinh nam và 18 học sinh nữ. Chọn ngẫu nhiên một học sinh. Xác suất chọn được 1 học sinh nữ là:
A. 1/38
B. 10/19
C. 9/19
D. 19/9
-
Câu 19:
Phép thử ngẫu nhiên (gọi tắt là phép thử) là gì?
A. Hoạt động mà ta không thể biết trước được kết quả của nó;
B. Hoạt động mà ta có thể biết trước được kết quả của nó;
C. Hoạt động mà ta gieo xúc xắc;
D. Cả 3 phương án trên đều sai.
-
Câu 20:
Trong các thí nghiệm sau thí nghiệm nào không phải là phép thử ngẫu nhiên:
A. Gieo đồng tiền xem xuất hiện mặt ngửa hay mặt sấp;
B. Gieo 3 đồng tiền và xem có mấy đồng tiền lật ngửa;
C. Chọn bất kì 1 học sinh trong lớp và xem là nam hay nữ;
D. Bỏ hai viên bi xanh và ba viên bi đỏ trong một chiếc hộp, sau đó lấy từng viên một để đếm xem có tất cả bao nhiêu viên bi.
-
Câu 21:
Cho tam thức bậc hai f(x) = ax\(^2\) + bx + c có đồ thị như hình vẽ dưới đây
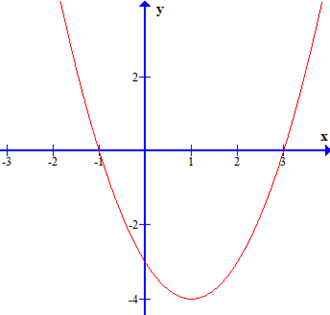
Bảng biến thiên của tam thức bậc hai là
A.

B.

C.
.png)
D.

-
Câu 22:
Cho phương trình \(x^2\) – 2x – m = 0. Tìm tất cả các giá trị của m để phương trình có 2 nghiệm thỏa mãn \(x_1 < x_2 < 2\).
A. m > 0;
B. m > 0;
C. – 1 < m < 0;
D. m > 1.
-
Câu 23:
Cho phương trình \(\sqrt {{x^2} + 3} = \sqrt {2x + 6} \). Chọn khẳng định đúng:
A. Phương trình có hai nghiệm phân biệt cùng dấu;
B. Phương trình có hai nghiệm phân biệt trái dấu;
C. Phương trình có một nghiệm;
D. Phương trình vô nghiệm.
-
Câu 24:
Tập nghiệm của phương trình \(\sqrt {\left( {x - 3} \right)\left( {2 - x} \right)} = \sqrt {4{x^2} + 12x + 9} \) là:
A. {10; 3};
B. {5};
C. {3};
D. ∅.
-
Câu 25:
Giả sử ta dùng 5 màu để tô cho 3 nước khác nhau trên bản đồ và không có màu nào được dùng hai lần. Số các cách để chọn những màu cần dùng là:
A. 60;
B. 8;
C. 15;
D. 53.
-
Câu 26:
Có bao nhiêu cách xếp 5 người thành một hàng dọc
A. 120;
B. 5;
C. 20;
D. 25.
-
Câu 27:
Chọn ngẫu nhiên một số nguyên dương không lớn hơn 15. Hãy mô ta không gian mẫu trên?
A. Ω = {1; 2; 3; 4; 5; 6; 7; 10; 11; 12; 13; 14; 15};
B. Ω = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14};
C. Ω = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14};
D. Ω = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15}.
-
Câu 28:
Từ các chữ số 1; 2; 4; 6; 8; 9 lấy ngẫu nhiễn một số. Xác suất để lấy được một số nguyên tố là:
A. 1/2
B. 1/3
C. 1/4
D. 1/6
-
Câu 29:
Có 3 chiếc hộp, hộp A chứa 1 chiếc bút xanh, 1 chiếc bút đỏ; hộp B chứa 1 chiếc bút đỏ, 1 chiếc bút tím; hộp C chứa 1 chiếc bút đỏ, 1 chiếc bút tím. Lấy ngẫu nhiên từ mỗi hộp 1 chiếc bút. Ta có sơ đồ cây sau:
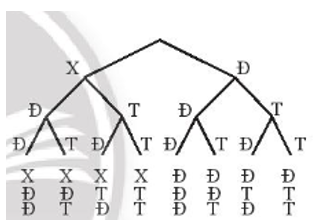
Dựa vào sơ đồ cây cho biết số kết quả thuận lợi cho biến cố H: “Trong 3 bút lấy ra có đúng 1 bút đỏ”.
A. 1
B. 2
C. 3
D. 8
-
Câu 30:
Cho phương trình \(x^2 + y^2\) – 2mx – 4(m – 2)y + 6 – m = 0. Điều kiện của m để phương trình đã cho là một phương trình đường tròn là:
A. m ∈ ℝ;
B. m∈(−∞;1)∪(2;+∞)
C. m∈(−∞;1]∪[2;+∞)
D. m∈(−∞;1/3)∪(2;+∞)











