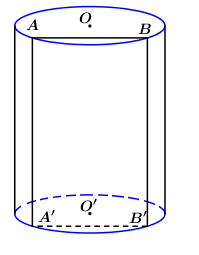
Cắt một khối trụ bởi một mặt phẳng ta được một khối \(\left( H \right)\) như hình vẽ bên. Biết rằng thiết diện là một hình elip có độ dài trục lớn bằng 8, khoảng cách từ điểm thuộc thiết diện gần mặt đáy nhất và điểm thuộc thiết diện xa mặt đáy nhất tới mặt đáy lần lượt là 8 và 14 (xem hình vẽ).Tính thể tích của \(\left( H \right)\).

Câu hỏi liên quan

• Cho hình nón có góc ở đỉnh bằng 120⁰ và đường cao bằng (2. ) Tính diện tích xung quanh của hình nón đã cho.

• Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có AB = 2AD = 2a, SA vuông góc với đáy, SA = a. Bán kính mặt cầu ngoại tiếp hình chóp là:

  

• Cho hình trụ có đường cao h và bán kính đáy là r. Trong các khối lăng trụ tứ giác nội tiếp hình trụ thì khối lăng trụ có thể tích lớn nhất bằng:

ZUNIA12

• Hình trụ có bán kính đáy bằng a và chiều cao bằng \(a\sqrt 3 \). Khi đó diện tích toàn phần của hình trụ bằng

• Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng 2a. Diện tích xung quanh của hình nón đỉnh S và đáy là hình tròn nội tiếp ABCD là

• Một hình trụ (T ) có diện tích  xung quanh bằng \(4\pi\) và  thiết diện qua  trục  của hình trụ này là một hình vuông. Diện tích toàn phần của (T ) là

   

• Cắt khối nón bởi một mặt phẳng qua trục tạo thành một tam giác ABC đều có cạnh bằng a, biết B, C thuộc đường tròn đáy. Thể tích của khối nón là:

• Cho hai hình vuông cùng có cạnh bằng 5 được xếp chồng lên nhau sao cho đỉnh X của một hình vuông là tâm của hình vuông còn lại (như hình vẽ bên). Tính thể tích V của vật thể tròn xoay khi quay mô hình trên xung quanh trục XY.

  

• Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Hãy tính diện tích xung quanh của hình nón có đỉnh là tâm O của hình vuông A’B’C’D’ và đáy là hình tròn nội tiếp hình vuông ABCD. Đáp án là:

• Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và góc giữa mặt bên và đáy bằng \(60^o\) . Thể tích khối nón nội tiếp trong hình chóp là: 

• Cho hình chữ nhật ABCD có AC = 2AD = 2a. Quay quanh trục AB đường gấp khúc ADCB ta được hình trụ có diện tích xung quanh là:

• Có ba quả bóng đá hình cầu có cùng bán kính r được xếp tiếp xúc với nhau từng đôi một. Trong các rổ hình trụ có chiều cao 2r và bán kính R, hỏi bán kính R nhỏ nhất là bao nhiêu để hình trụ có thể chứa được cả ba quả bóng đó?

• Cho khối nón có bán kính đáy r = 2, chiều cao \(h = \sqrt 3 .\) Thể tích của khối nón là

• Cho khối nón có bán kính đáy và đường sinh lần lượt là r = 3cm,l = 5cm. Tính thể tích khối nón.

• Một hình trụ có diện tích xung quanh là (\(16\pi \)), thiết diện qua trục là hình vuông. Một mặt phẳng ( \(\alpha \)) song song với trục, cắt hình trụ theo thiết diện là (ABB'A' ), biết một cạnh thiết diện là một dây của đường tròn đáy hình trụ và căng một cung 120⁰. Chu vi tứ giác (ABB'A' ) bằng:

  

• Cho hình chóp đều S.ABC có cạnh đáy AB=q , cạnh bên hợp với mặt đáy một góc \(60^o\) . Bán kính hình cầu ngoại tiếp hình chóp S.ABC là

• Cho khối hộp chữ nhật ABCD.A'B'C'D' có đáy là hình vuông, BD = 2a góc giữa hai mặt phẳng (A'BD) và (ABCD) bằng 30⁰. Thể tích của khối hộp chữ nhật đã cho bằng

• Cho hình chữ nhật (ABCD ), khi quay hình chữ nhật quanh cạnh (AB ) thì (CD ) được gọi là:

• Cho đường tròn tâm O bán kính r′. Xét hình chóp S.ABCD có SA vuông góc với mặt phẳng đáy, S và A cố định, SA=h cho trước và có đáy ABCD là một tứ giác tùy ý nội tiếp đường tròn đã cho, trong đó các đường chéo AC và BD vuông góc với nhau. Hỏi đáy ABCD là hình gì để thể tích hình chóp đạt giá trị lớn nhất?

• Cho đường thẳng a và điểm A cách đường thẳng a một khoảng bằng 4cm. Trong các mặt cầu đi qua A và tiếp xúc với đường thẳng a, mặt cầu (S) có diện tích nhỏ nhất thì diện tích đó bằng: