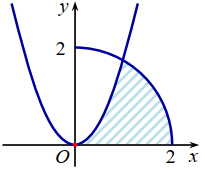
Cho (H ) là hình phẳng giới hạn bởi parabol \(y=\sqrt{3} x^{2}\), cung tròn có phương trình \(y=\sqrt{4-x^{2}} \quad(\text { vói } 0 \leq x \leq 2)\) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của (H ) bằng

Câu hỏi liên quan

• Cho hàm số y = f( x) = ax⁴+ bx²+ c (a > 0) có đồ thị (C), đồ thị hàm số y = f’(x). Đồ thị hàm số y = f( x) tiếp xúc với trục hoành tại hai điểm. Tính diện tích của hình phẳng giới hạn bởi đồ thị (C) và trục hoành?

  

• Tính  tích phân sau \(J = \mathop \smallint \nolimits_2^7 \frac{{xdx}}{{\sqrt {x + 2}  + \sqrt {x - 2} }}\)

• Cho m thỏa mãn \(\mathop \smallint \nolimits_1^2 \left[ {{m^2} + \left( {4 - 4m} \right)x\; + 4{x^3}} \right]dx\; = \;\mathop \smallint \nolimits_2^4 2xdx\). Nghiệm của phương trình \({\log _3}\;\left( {x + m} \right)\; = \;1\) là:

ZUNIA12

• Tích phân \(\int_{0}^{2} \frac{x}{x^{2}+3} d x\) bằng?

• Tính tích phân \(I = \mathop \smallint \nolimits_0^{\rm{\pi }} {\sin ^2}x.{\cos ^2}xdx\)

• Cho hàm số \(f(x)\) xác định trên \(\mathbb{R}\backslash \left\{ -2;1 \right\}\) thỏa mãn \({f}'\left( x \right)=\frac{1}{{{x}^{2}}+x-2},f\left( -3 \right)-f\left( 3 \right)=0,f\left( 0 \right)=\frac{1}{3}\). Giá trị của biểu thức \(f\left( -4 \right)+f\left( 1 \right)-f\left( 4 \right)\) bằng

• Tính diện tích hình phẳng giới hạn bởi đồ thị các hàm số y = x² , y = 4x - 4 và y = -4x - 4

• Cho hàm số \(f(x) = \left\{ \begin{array}{l} 3x + 3\,\,\,{\rm{khi }}x < \frac{1}{2}\\ x + 4\,\,\,\,\,{\rm{khi }}x \ge \frac{1}{2} \end{array} \right.\). Tính tích phân \(\int\limits_{0}^{\frac{\pi }{2}}{f\left( \sin x \right)}\cos x\text{d}x\).

• Biết \(\int\limits_{0}^{4} \frac{\sqrt{2 x+1} \mathrm{d} x}{2 x+3 \sqrt{2 x+1}+3}=a+b \ln 2+c \ln \frac{5}{3}(a, b, c \in \mathbb{Z}) . \text { Tính } T=2 a+b+c\)

• Cho hàm số y=f(x) có đạo hàm liên tục trên [0;1] thỏa mãn \(3 f(x)+x \cdot f^{\prime}(x) \geq x^{2018} \quad \forall x \in[0 ; 1]\). Tìm giá trị nhỏ nhất của \(\int_{0}^{1} f(x) \mathrm{d} x\)

• Giá trị của tích phân \(\int_{0}^{1} \frac{4 x+2}{x^{2}+x+1}dx\) là

• Cho hàm số y =f(x) có đạo hàm liên tục trên đoạn [1;2] thỏa mãn \(f(1)=\) và \(f(x)-(x+1) f^{\prime}(x)=2 x f^{2}(x), \forall x \in[1 ; 2]\) Giá trị của \(\int_{1}^{2} f(x) d x\) bằng?

• Nếu \(\begin{equation} \int_{-1}^{4}[5 f(x)-3] \mathrm{d} x=5 \text { thì } \int_{-1}^{4} f x \mathrm{~d} x \text { bằng } \end{equation}\)

• Tích phân \(I=\int_{1}^{\sqrt[4]{3}} \frac{1}{x\left(x^{4}+1\right)} d x\) bằng
   

• Cho hình phẳng (H ) giới hạn bởi các đường \(y=\sqrt{x}-1\), trục hoành và đường thẳng x = 4 . Khối tròn xoay tạo thành khi quay (H ) quanh trục hoành có thể tích V bằng bao nhiêu?

• Cho \(\int_{1}^{2} \frac{1}{\sqrt{x^{2}+1}} d x=\ln \frac{2+\sqrt{a}}{1+\sqrt{b}}, a\, \mathrm{và}\, b\) là các số hữu tỉ. Giá trị của \(a\over b\) là:

• Thể tích của vật tròn xoay có được khi quay hình phẳng giới hạn bởi đồ thị hàm y =tan x , trục Ox , đường thẳng x = 0 , đường thẳng \(x=\frac{\pi}{3}\)  quanh trục Ox  là:

• Tích phân \(I=\int\limits_{0}^{\sqrt[3]{7}} \frac{3 x^{5}}{\sqrt[3]{8-x^{3}}} d x\) có giá trị là:

• Biết tích phân \(I_{1}=\int_{0}^{1} 2 x d x=a\) . Giá trị của là \(I_{2}=\int_{a}^{2}\left(x^{2}+2 x\right) d x\) là:

• Thể tích khối tròn xoay khi quay hình phẳng (H ) giới hạn bởi\(y=x^{2}\text{ và }y=x+2\) quanh trục Ox là