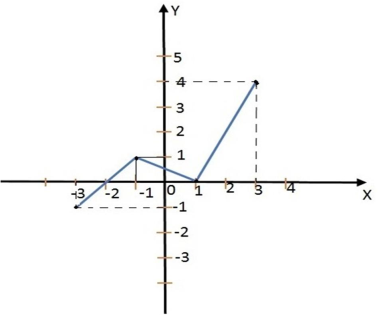
Cho hàm số đa thức f (x) có đạo hàm tràm trên R . Biết f(0)=0 và đồ thị hàm số \(y=f^{\prime}(x)\) như hình sau.
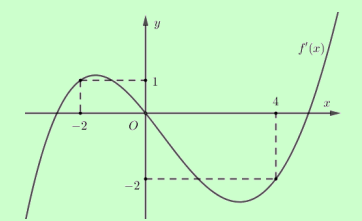
Hàm số \(g(x)=\left|4 f(x)+x^{2}\right| \) đồng biến trên khoảng nào dưới đây
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo saiXét hàm số \(h(x)=4 f(x)+x^{2}, x \in R\) ,
\(h^{\prime}(x)=4 f^{\prime}(x)+2 x \Rightarrow h^{\prime}(x)=0 \Leftrightarrow f^{\prime}(x)=-\frac{x}{2}\)
Vẽ đường thẳng \(y=-\frac{x}{2}\) trên cùng hệ trục Oxy với đồ thị \(y=f^{\prime}(x)\) như hình vẽ sau
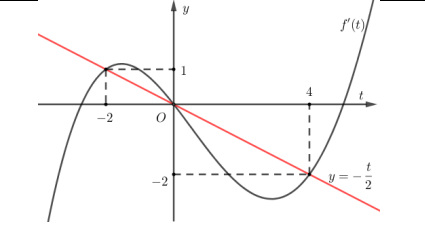
Từ đồ thị ta có BBT của h(x) như sau :

Chú ý ở đây\(h(0)=4 f(0)=0\)
Từ đó ta có BBT của g(x) như sau :
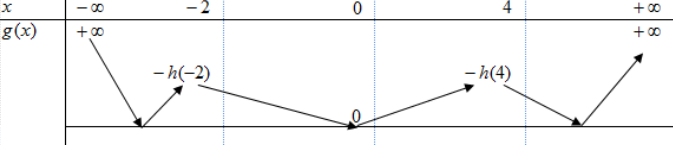
Từ BBT ta suy ra g(x) đồng biến trên khoảng (0;4)
ADMICRO
YOMEDIA
ZUNIA9
.png)
.PNG)











