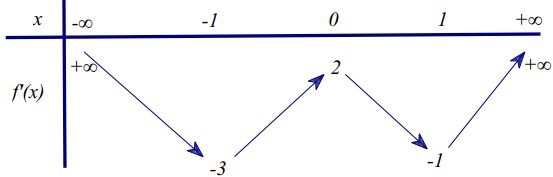
Cho hàm số \(y = f\left( x \right)\) là một hàm đa thức có bảng xét dấu \(f’\left( x \right)\) như sau

Số điểm cực trị của hàm số \(g\left( x \right) = f\left( {{x^2} – \left| x \right|} \right)\)

Câu hỏi liên quan

• Có bao nhiêu mệnh đề đúng trong các phát biểu sau?

  1. Hàm số không có đạo hàm tại x = 0.

  2. Hàm số không liên tục tại x = 0.

  3. Hàm số không có cực trị tại x = 0.

  4. Hàm số đạt cực trị tại x = 0.

• Hàm số \(y = a\sin 2x + b\cos 3x - 2x\;(0 < x < 2{\rm{\pi }})\) đạt cực trị tại \(x = \frac{{\rm{\pi }}}{2};x = {\rm{\pi }}\). Khi đó, giá trị của biểu thức \(P = a + 3b - 3ab\) là:

• Cho hàm số y = f(x)  có bảng biến thiên như hình bên. Mệnh đề nào dưới đây đúng?

  

ZUNIA12

• Cho hàm số \(f(x)\) , bảng biến thiên của hàm số \(f'(x)\) như sau

  

  Số điểm cực trị của hàm số \(y=f\left(x^{2}+2 x\right)\) là

• Đồ thị của hàm số y = 3x⁴ – 4x³ – 6x² + 12x + 1 đạt cực tiểu tại M(x₁; y₁). Tính tổng x₁ + y₁

• Tìm tập hợp tất cả giá trị thực của tham số  m  để hàm số \(y=-\frac{1}{3}mx^3-x^2+mx\) có cực trị

   

• Hàm số  y=f(x) có \(f'\left( x \right) = \left( {2x + 7} \right){\left( {x - 3} \right)^4}\left( {x + 1} \right)\). Số điểm cực trị của hàm số là:

• Cho hàm số y=f(x) có \(f'\left( x \right) = 2{x^2}\left( {x + 1} \right)\left( { - x + 3} \right)\left( {x - 2} \right)\). Điểm cực tiểu của hàm số là

   

   

   

• Cho hàm số y = x⁴- 2( 1 - m²) x²+ m+1. Tồn tại giác trị của m  để  hàm số có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số lập thành tam giác có diện tích lớn nhất . Khi đó khẳng định nào đúng?

• Tìm tất cả các giá trị của tham số m để đồ thị hàm số \(y = {x^3} - 3\left( {m + 1} \right){x^2} + 12mx - 3m + 4\left( C \right)\) có hai điểm cực trị là A và B sao cho hai điểm này cùng với điểm \(C\left( { - 1; - \frac{9}{2}} \right)\) lập thành tam giác nhận gốc tọa độ O làm trọng tâm

• Tìm điểm cực tiểu của hàm số \(y = \frac{1}{3}{x^3} – 2{x^2} + 3x + 1\)

• Hàm số  y=f(x) có \(f'\left( x \right) = \left( {2x + 1} \right){\left( {x - 2} \right)^4}\). Số điểm cực trị của hàm số là:

• Cho hàm số y=f(x) có \(f'\left( x \right) = - \left( {3x + 1} \right){\left( {x + 1} \right)^2}{\left( {x - 3} \right)^3}\left( {x + 4} \right)\). Điểm cực đại của hàm số là

• Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số \(y=-x^{3}+3 m x+1\) có 2 điểm cực trị A, B sao cho tam giác OAB vuông tại O ( với O là gốc tọa độ )
   

• Điểm cực tiểu của hàm số \(y = 2{x^4} - {x^2} - 1\) là:

• Cho hàm số bậc bốn f(x) có bảng biến thiên như sau

  

  Số điểm cực trị của hàm số \(g(x) = {x^2}{\left[ {f(x + 1)} \right]^4}\)

• Gọi S là tập hợp tất cả các giá trị thực của tham số m để hàm số \(y = \frac{1}{3}{x^3} - m{x^2} + \left( {{m^2} - 1} \right)x\) có hai điểm cực trị A và B sao cho A, B nằm khác phía và cách đều đường thẳng d: y= 5x- 9 . Tính tổng tất cả các phần tử của S.

• Số cực trị của hàm số \(f\left( x \right) = - \frac{1}{2}{{\rm{x}}^4} + \frac{1}{3}{{\rm{x}}^2} - 2\) là

• Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right) = \left( {x – 1} \right)\left( {x + 3} \right)\). Số điểm cực tiểu của hàm số là

• Cho hàm số y=f(x) có \(f'\left( x \right) = {\left( {5 - x} \right)^2}{\left( {x + 1} \right)^3}\left( {3 + x} \right)\). Điểm cực đại của hàm số là