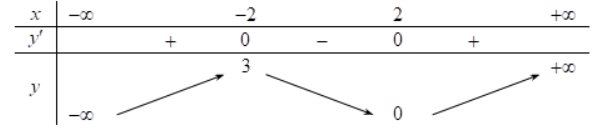
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) có đạo hàm \(f’\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng xét dấu như hình vẽ bên
.png)
Hỏi hàm số \(y = f\left( {{x^2} – 2\left| x \right|} \right)\) có tất cả bao nhiêu điểm cực trị
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTập xác định của hàm số: \(D=\mathbb{R}\)
* \(y = h\left( x \right) = f\left( {{{\left| x \right|}^2} – 2\left| x \right|} \right)\)
\(y’ = h’\left( x \right) = f’\left( {{{\left| x \right|}^2} – 2\left| x \right|} \right).\frac{x}{{\left| x \right|}}.\left( {2\left| x \right| – 2} \right).\)
\(h’\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = – 1\\{\left| x \right|^2} – 2\left| x \right| = 0\\{\left| x \right|^2} – 2\left| x \right| = 1\\{\left| x \right|^2} – 2\left| x \right| = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = – 1\\x = 2\\x = – 2\\x = 1 + \sqrt 2 \\x = – 1 – \sqrt 2 \\x = 1 + \sqrt 3 \\x = – 1 – \sqrt 3\end{array} \right.\).
Ta thấy phương trình \(h’\left( x \right) = 0\) có 8 nghiệm đơn \(\left( 1 \right)\).
\(h’\left( x \right)\) không tồn tại tại x = 0 mà x = 0 thuộc tập xác định đồng thời qua đó \(h’\left( x \right)\) đổi dấu \(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra hàm số đã cho có 9 điểm cực trị.
Câu hỏi liên quan
-
Hàm số \(y = {x^3}{\left( {1 – x} \right)^2}\) có
-
Hàm số y=f(x) có \(f'\left( x \right) = \left( {2x + 1} \right){x^3}{\left( {x + 1} \right)^2}\left( {3x - 1} \right)\). Số điểm cực trị của hàm số là:
-
Cho hàm số y = f(x) có đồ thị như hình bên. Hàm số có bao nhiêu điểm cực tiểu trên khoảng \(\left( {a;b} \right)\)?
.jpg.png)
-
Số cực trị của hàm số \(f\left( x \right) = - 4{{\rm{x}}^4} - 2{{\rm{x}}^2} + 4\) là
-
Cho hàm số y= f( x) có bảng biến thiên như sau
Tìm giá trị cực đại và giá trị cực tiểu của hàm số đã cho.
-
Số điểm cực tiểu của hàm số \(f\left( x \right) = - \frac{1}{2}{{\rm{x}}^4} + \frac{1}{3}{{\rm{x}}^2} - 2\) là
-
Hàm số \(y = 2{x^4} - {x^2} - 1\) có điểm cực đại là:
-
Điểm cực đại của đồ thị hàm số \(y = {x^3} + 3{x^2} + 2\) là
-
Cho hàm số y = f(x) có đồ thị như hình vẽ. Điểm cực đại của đồ thị hàm số là
-
Trong các hàm số dưới đây, hàm số nào có đúng 2 cực trị?
-
Hàm số nào sau đây có cực trị?
-
Hàm số \(y = – {x^4} + 2{x^2} – 3\) có điểm cực đại và điểm cực tiểu \({x_{CT}}\,\) là.
-
Cho hàm số \(y=f(x)\) có bảng biến thiên như hình vẽ. Hàm số có bao nhiêu điểm cực trị?
-
Cho hàm số y = f (x) xác định, liên tục trên \(\mathbb{R}\)và có bảng biến thiên sau
Khẳng định nào sau đây sai?
-
Đồ thị hàm số \(y = {x^3} - 6{x^2} + 9x - 1\) có tọa độ điểm cực đại là
-
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ. Hàm số có bao nhiêu điểm cực trị?
.png)
-
Cho hàm số y = x3-3x2. Tìm tất cả các giá trị thực tham số m để đường thẳng đi qua 2 điểm cực trị của đồ thị C tạo với đường thẳng x+ my+ 3 = 0 một góc α biết \(\cos \alpha = \frac{4}{5}\).
-
Hàm số \(y = - 3\sqrt[3]{{{x^2}}} + 2\) có bao nhiêu cực đại?
-
Hàm số \(y = {x^4} - 3{x^2} - 1\) có bao nhiêu điểm cực trị?
-
Số điểm cực đại của hàm số \(f\left( x \right) = - \frac{3}{2}{{\rm{x}}^4}{\rm{ - 3}}{{\rm{x}}^2} - 1\) là
