Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\). Đồ thị của hàm số \(y = f’\left( x \right)\) như hình bên. Đặt \(g\left( x \right) = 2f\left( x \right) – {\left( {x + 1} \right)^2}\). Mệnh đề nào dưới đây đúng?
.jpg.png)
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có \(g’\left( x \right) = 2f’\left( x \right) – 2\left( {x + 1} \right) = 0 \Leftrightarrow f’\left( x \right) – \left( {x + 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = – 3\\x = 1\\x = x\end{array} \right.\).
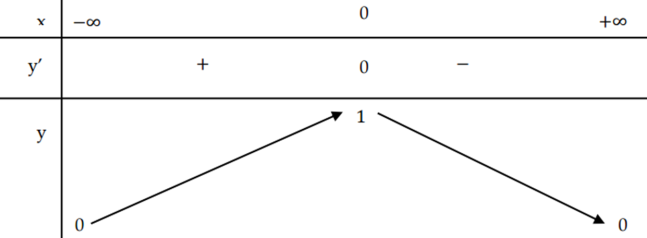
Từ đồ thị của hàm số \(y = f’\left( x \right)\) suy ra bảng biến thiên \(g\left( x \right) = 2f\left( x \right) – {\left( {x + 1} \right)^2}\)
.png)
Do đó Mệnh đề nào dưới đây đúng \(\mathop {Max}\limits_{\left[ { – 3;\,3} \right]} g\left( x \right) = g\left( 1 \right)\).
.jpg.png)
.jpg.png)
.png)











