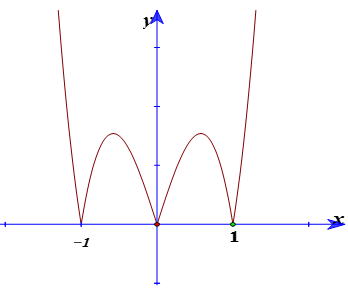
Cho hàm số y = f( x) = ax⁴+ bx²+ c (a > 0) có đồ thị (C), đồ thị hàm số y = f’(x). Đồ thị hàm số y = f( x) tiếp xúc với trục hoành tại hai điểm. Tính diện tích của hình phẳng giới hạn bởi đồ thị (C) và trục hoành?

Tích phân \(I=\int_{1}^{a} \frac{x^{2}+1}{x^{3}+3 x} d x=\frac{1}{3} \ln \frac{7}{2}\) . Giá trị của a là

Biết \(I_{1}=\int_{\frac{\pi}{3}}^{\frac{\pi}{2}} \sin x d x=a\) . Giá trị của \(I_{2}=\int_{a}^{1} \frac{x^{2}+1}{x^{3}+x} d x=b \ln 2-c \ln 5\). Thương số của b với c là?

Cho hàm số f liên tục trên \(\mathbb{R}\) và hai số thực a<b . Nếu \(\int_{a}^{b} f(x) d x=\alpha\) thì tích phân \(\int\limits_{a / 2}^{b / 2} f(2 x) d x\) có giá trị bằng

Tính \(I = \mathop \smallint \nolimits_{ - 1}^2 2xdx\). Chọn kết quả đúng:

Cho hàm số f(x) liên tục trên ℝ và thỏa mãn\(f(1+2 x)+f(1-2 x)=\frac{x^{2}}{x^{2}+1}, \forall x \in \mathbb{R}\) . Tính tích phân \(I=\int_{-1}^{3} f(x) d x\)

Giả sử \(\mathop \smallint \nolimits_a^b f\left( x \right)dx = 2\;,\;\mathop \smallint \nolimits_c^b f\left( x \right)dx = 3\;\) và a < b < c thì \(\mathop \smallint \nolimits_a^c f\left( x \right)dx\) bằng bao nhiêu ?

Cho hai hàm số \(f\left( x \right),g\left( x \right)\) liên tục trên \(\left[ {1;3} \right]\) thỏa mãn \(\int\limits_1^3 {f\left( x \right)} dx = 1, \int\limits_1^3 {g\left( x \right)} dx = 3\). Tính \(\int\limits_3^1 {\left[ {f\left( x \right) – 2g\left( x \right)} \right]} dx\)?

Cho \(\int_{0}^{1} \frac{\mathrm{d} x}{\sqrt{x+2}+\sqrt{x+1}}=a \sqrt{b}-\frac{8}{3} \sqrt{a}+\frac{2}{3},\left(a, b \in \mathbb{N}^{*}\right) . \text { Tính } a+2 b\)

Giá trị của tích phân \(I=\int_{0}^{\frac{\pi}{2}} \frac{\sin ^{2007} x}{\sin ^{2007} x+\cos ^{2007} x} d x\) là

Cho hàm số \(f\left( x \right)\) xác định trên \(\left[ {0;\frac{\pi }{2}} \right]\) thỏa mãn \(\int\limits_0^{\frac{\pi }{2}} {\left[ {{f^2}\left( x \right) – 2\sqrt 2 f\left( x \right)\sin \left( {x – \frac{\pi }{4}} \right)} \right]{\mathop{\rm d}\nolimits} x} = \frac{{2 – \pi }}{2}\). Tích phân \(\int\limits_0^{\frac{\pi }{2}} {f\left( x \right){\mathop{\rm d}\nolimits} x} \) bằng

Cho hàm số f(x) liên tục trên R thỏa mãn \(2 f^{3}(x)-3 f^{2}(x)+6 f(x)=x, \forall x \in \mathbb{R}\) . Tính tích phân \(I=\int_{0}^{5} f(x) \mathrm{d} x\)

Cho hàm số y = f(x) có đạo hàm f'(x) liên tục trên [0;2] và f(2) = 3 và \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8qCaeaaca % WGMbWaaeWaaeaacaWG4baacaGLOaGaayzkaaGaaeizaiaadIhaaSqa % aiaaicdaaeaacaaIYaaaniabgUIiYdGccqGH9aqpcaaIZaaaaa!40F4! \int\limits_0^2 {f\left( x \right){\rm{d}}x} = 3\). Tính \(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa8qCaeaaca % WG4bGaaiOlaiqadAgagaqbamaabmaabaGaamiEaaGaayjkaiaawMca % aiaabsgacaWG4baaleaacaaIWaaabaGaaGOmaaqdcqGHRiI8aaaa!40E2! \int\limits_0^2 {x.f'\left( x \right){\rm{d}}x} \)

Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và thỏa \(\int\limits_{ – 2}^2 {f\left( {\sqrt {{x^2} + 5} – x} \right){\rm{d}}x} = 1,\int\limits_1^5 {\frac{{f\left( x \right)}}{{{x^2}}}{\rm{d}}x} = 3.\) Tính \(\int\limits_1^5 {f\left( x \right){\rm{d}}x} .\)

Tích phân: \(J = \mathop \smallint \nolimits_0^1 \frac{{xdx}}{{{{\left( {x + 1} \right)}^3}}}dx\) bằng

Biết \(I=\int_{0}^{1}(2 x+3) e^{x} \mathrm{d} x=a e+b, \text { với } a, b\) là các số hữu tỉ. Mệnh đề nào sau đây là mệnh đề đúng?

Tìm a để \(\int_{1}^{2}(3-a x) d x=-3\) ?

Cho hàm số y=f(x) thỏa mãn \(f\left(x^{3}+3 x+1\right)=3 x+2, \forall x \in \mathbb{R} . \text { Tính } I=\int_{1}^{5} x \cdot f^{\prime}(x) d x\)

Giá trị của tích phân \(I=\int\limits_{0}^{3} \frac{2 x^{2}+x-1}{\sqrt{x+1}} d x\) là

Tính tích phân \(I=\int_{0}^{\frac{\pi}{2}} \sin \left(\frac{\pi}{4}-x\right) \mathrm{d} x\)

Cho hàm số y=f(x) có đạo hàm liên tục trên \((0 ;+\infty)\) thỏa mãn \(x^{2} f^{\prime}(x)+f(x)=0 \text { và } f(x) \neq 0, \forall x \in(0 ;+\infty)\). Tính \(f(2) \text { biết } f(1)=\mathrm{e}\)