Cho hình chóp S ABC . có đáy là tam giác vuông cân tại C, AB = 3. Hình chiếu vuông góc của S xuống mặt đáy trùng với trọng tâm của tam giác ABC và \(S B=\frac{\sqrt{14}}{2}\). Thể tích của khối chóp đã cho bằng
 

Câu hỏi liên quan

• Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = a, OB = b, OC = c. Tính thể tích khối tứ diện OABC.

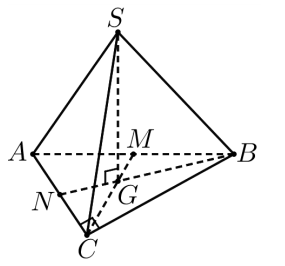
• Cho khối tứ diện \(OABC\) với \(OA,\,\,OB,\,\,OC\) vuông góc từng đôi một và \(OA=a,\text{ }OB=2a,\text{ }OC=3a.\) Gọi M, N lần lượt là trung điểm của hai cạnh \(AC,\,\,BC.\) Thể tích của khối tứ diện \(OCMN\) tính theo a bằng:

• Khối lập phương có đường chéo bằng 2a thì có thể tích là.

ZUNIA12

• Tính thể tích của khối hộp chữ nhật ABCD.A’B’C’D’ có AB = 3, AD = 4, AA’ = 5.

• Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a, khoảng cách giữa hai đường thẳng SA và CD bằng \(a\sqrt 3 \). Tính thể tích khối chóp S.ABCD.

• Tính thể tích của khối lập phương có cạnh bằng 2.

• Cho hình lăng trụ \(ABC.ABC\) có đáy ABC là tam giác đều cạnh a, hình chiếu của C’ trên (ABC) là trung điểm I của \(BC.\) Góc giữa AA’ và BC là 30^o. Thể tích của khối lăng trụ \(ABC.ABC\):

• Cho hình vuông ABCD có cạnh a, M là trung điểm của AD. Xét khối tròn xoay sinh bởi tam giác CDM (cùng các điểm trong của nó) khi quay quanh đường thẳng AB. Thể tích của khối tròn xoay đó bằng

• Cho hình lăng trụ ABC.A'B'C' có ABC là tam giác vuông tại A. Hình chiếu của A' lên (ABC) là trung điểm của BC. Tính thể tích V của khối lăng trụ ABC.A'B'C' biết AB = a, AC = \(a\sqrt 3 \), AA' = 2a.

• Cho hình lăng trụ đều \(ABC.{A}'{B}'{C}'\). Mặt phẳng \(({A}'BC)\) tạo với mặt phẳng (ABC) một góc \(30{}^\circ \) và tam giác \({A}'BC\) có diện tích bằng \(8{{a}^{2}}\). Tính thể tích khối lăng trụ \(ABC.{A}'{B}'{C}'\).

• Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, AB = a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết góc giữa SB và mặt phẳng (ABC) bằng 45⁰.

• Cho hình chóp S.ABC có đáy là ABC là tam giác vuông cân tại B và BA = BC = a. Cạnh bên \( SA = a\sqrt 3 \) vuông góc với mặt phẳng (ABC). Tính thể tích V của khối chóp S.ABC.

• Một khối lăng trụ tam giác đều cạnh đáy bằng \(a,\) góc giữa đường chéo mỗi mặt bên và mặt đáy bằng \({{60}^{0}}.\) Tính thể tích khối trụ ngoại tiếp khối lăng trụ đó.

• Thể tích của khối lăng trụ có khoảng cách giữa một đường thẳng bất kì của đáy này tới một đường thẳng bất kì của đáy kia bằng h và diện tích đáy bằng B là

• Cho hình chóp \(S.ABCD\) có đáy ABCD là hình chữ nhật, AB=a, BC=2a, đường thẳng \(SA\) vuông góc với mặt phẳng \(\left( ABCD \right)\) và \(SA=3a\). Thể tích của khối chóp \(S.ABCD\) bằng

• Cho khối chóp S.ABCD có đáy là hình chữ nhật, \(SA \bot \left( {ABCD} \right),AB = 3a, AD = 2a, SB = 5a.\) Tính thể tích V của khối chóp S.ABCD theo a.

• Khối lập phương ABCD.A’B’C’D’ có thể tích bằng \({{a}^{3}}\). Tính độ dài của A’C.

• Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, \(SA \bot \left( {ABCD} \right)\), SA = a. Gọi G là trọng tâm tam giác SCD. Tính thể tích khối chóp G.ABCD.

• Cho lăng trụ đứng \(ABC.A'B'C'\) có đáy là tam giác đều cạnh \(a\). Mặt phẳng \(\left( AB'C' \right)\) tạo với mặt đáy góc \({{60}^{0}}\). Tính theo \(a\) thể tích lăng trụ \(ABC.A'B'C'\).

• Cho khối hộp \(ABCD.A'B'C'D'\) có tất cả các cạnh bên bằng \(a\) và các góc \(A'AB,BDA,A'AD\) đều bằng \(\alpha \left( {{0}^{0}}<\alpha <{{90}^{0}} \right).\) Tính thể tích \(V\) của khối hộp.