Cho khối chóp \(S.ABCD\) có đáy là hình vuông cạnh a, \(SA\) vuông góc với đáy và \(SC\) tạo với mặt phẳng \(\left( SAB \right)\) một góc \({{30}^{0}}.\) Tính thể tích \(V\) của khối chóp đã cho.
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo sai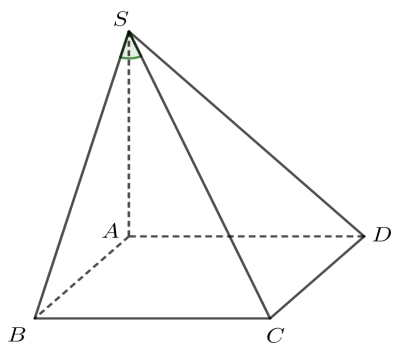
Ta có \(CB\bot \left( SAB \right)\Rightarrow \left[ SC;\left( SAB \right) \right]=\left( SC;SB \right)=\widehat{CSB}={{30}^{0}}\)
Suy ra \(SB=BC.\cot {{30}^{0}}=a\sqrt{3};\) \(SA=\sqrt{S{{B}^{2}}-A{{B}^{2}}}=a\sqrt{2}\)
Thể tích khối chóp : \(V=\frac{1}{3}{{S}_{ABCD}}.SA=\frac{\sqrt{2}{{a}^{3}}}{3}\).
ADMICRO
YOMEDIA
ZUNIA9
.png)
.png)











