Cho hai hình cầu đồng tâm \(\left( {O;2} \right)\) và \(\left( {O;\sqrt {10} } \right)\). Một tứ diện ABCD có hai đỉnh A, B nằm trên mặt cầu \(\left( {O;2} \right)\) và các đỉnh C, D nằm trên mặt cầu \(\left( {O;\sqrt {10} } \right)\). Thể tích lớn nhất của khối tứ diện ABCD bằng bao nhiêu?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai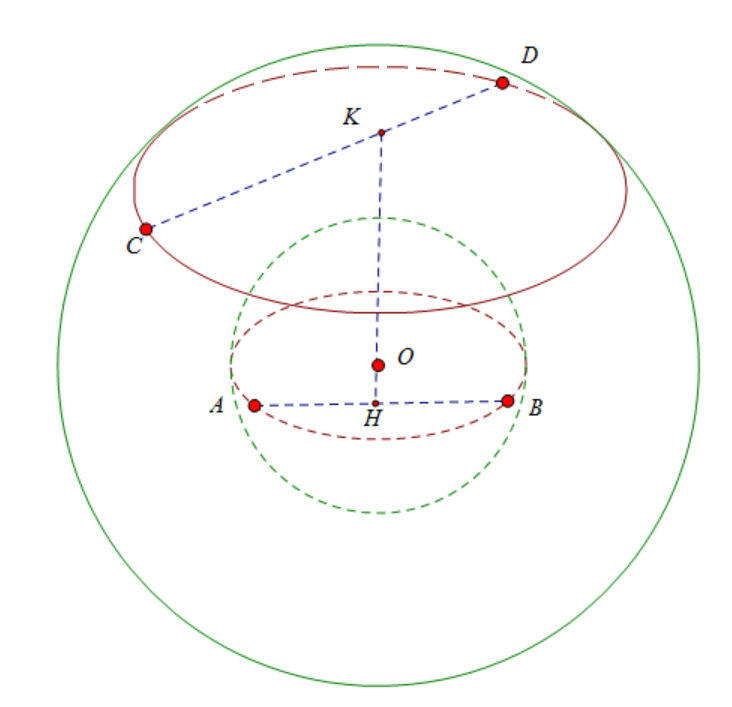
Đặt OK = a, OH = b.
\({V_{ABCD}} = \frac{{AB.CD.HK.\sin \left( {AB;CD} \right)}}{6} \le \frac{{AB.CD.HK}}{6} \le \frac{2}{3}\sqrt {10 – {a^2}} .\sqrt {4 – {b^2}} \left( {a + b} \right)\)
\({V_{ABCD}} \le \frac{2}{3}\frac{{\sqrt 3 }}{{\sqrt 2 }}\sqrt {\left( {10 – {a^2}} \right)\left( {4 – {b^2}} \right)\left( {{a^2} + 2{b^2}} \right)} \)
\({V_{ABCD}} \le \frac{{2\sqrt 3 }}{6}\sqrt {\left( {10 – {a^2}} \right)\left( {8 – 2{b^2}} \right)\left( {{a^2} + 2{b^2}} \right)} \)
\({V_{ABCD}} \le \frac{{2\sqrt 3 }}{6}\sqrt {216} = 6\sqrt 2 \). Dấu xảy ra khi a = 2, b = 1.











