Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Đường thẳng SA vuông góc đáy và mặt bên (SCD) hợp với đáy một góc bằn\(60^{\circ}\) Thể tích của khối chóp đã cho bằng
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo sai
Xác định: 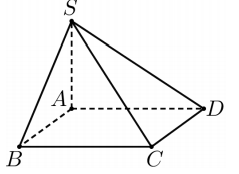 \(60^{0}=(\widehat{(S C D),(A B C D)})=(\widehat{S D, A D})=\widehat{S D A}\)
\(60^{0}=(\widehat{(S C D),(A B C D)})=(\widehat{S D, A D})=\widehat{S D A}\)
Chiều cao khối chóp: \(S A=A D \cdot \tan \widehat{S D A}=a \sqrt{3}\)
Diện tích hình vuông: \(S_{A B C \mathrm{D}}=A B^{2}=a^{2}\)
Vậy thể tích khối chóp: \(V_{S . A B C D}=\frac{1}{3} S_{A B C D} \cdot S A=\frac{a^{3} \sqrt{3}}{3}\)
ADMICRO
YOMEDIA
ZUNIA9











