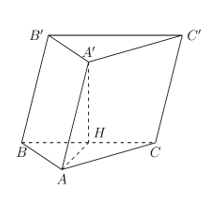
Cho hình lăng trụ ABC.A'B'C' có ABC là tam giác vuông tại  A. Hình chiếu của A' lên (ABC) là trung điểm của BC. Tính thể tích V của khối lăng trụ ABC.A'B'C' biết AB = a, \(AC = a\sqrt 3 \), AA' = 2a

Câu hỏi liên quan

• Cho hình lập phương ABCD.A’B’C’D’ với O’ là tâm hình vuông A’B’C’D’. Biết rằng tứ diện O’.BCD có thể tích bằng \(6{a^3}\). Tính thể tích V của khối lập phương ABCD.A’B’C’D’.

• Cho hình chóp S ABCD . có đáy là hình vuông tâm O, BD =1. Hình chiếu vuông góc H của đỉnh S trên mặt phẳng đáy (ABCD) là trung điểm OD. Đường thẳng SD tạo với mặt phẳng đáy một góc 60⁰ Thể tích của khối chóp đã cho bằng

• Cho khối lăng trụ có diện tích đáy bằng \({a^2}\sqrt 3 \), khoảng cách giữa hai đáy của lăng trụ bằng \(a\sqrt 6 \). Tính thể tích V của khối lăng trụ

ZUNIA12

• Cho hình chóp S.ABC có cạnh bên SA vuông góc với mặt phẳng đáy \(\left( {ABC} \right)\). Biết SA = a, tam giác ABC là tam giác vuông cân tại A, AB = 2a. Tính theo a thể tích V của khối chóp S.ABC.

• Cho tứ diện đều ABCD cạnh a. Thể tích của khối tứ diện ABCD là:

• Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, \(SA \bot \left( {ABCD} \right)\), SA = a. Gọi G là trọng tâm tam giác SCD. Tính thể tích khối chóp G.ABCD.

• Cho hình lăng trụ ABC.A’B’C’, đáy ABC có \(AC=a\sqrt{3};BC=3a,\widehat{ACB}={{30}^{0}}\). Cạnh bên hợp với mặt phẳng đáy góc \({{60}^{0}}\) và mặt phẳng (A’BC) vuông góc với mặt phẳng (ABC). Điểm H trên cạnh BC sao cho BC=3BH và mặt phẳng (A’AH) vuông góc với mặt phẳng (ABC). Thể tích khối lăng trụ ABC.A’B’C’ bằng:

• Cho hình chóp S.ABCD có đáy là hình chữ nhật. Tính thể tích V của hình chóp S.ABCD biết AB = a, AD = 3a, SA = 2a.

• Hình chóp S.ABC có A’B’C’ lần lượt là trung điểm của SA, SB, SC; tỷ số thể tích của hai khối chóp SA’B’C’ và SABC là:

• Cho hình lập phương ABCD.A’B’C’D’ có diện tích mặt chéo ACC’A’ bằng \(2\sqrt 2 {a^2}\). Thể tích của khối lập phương ABCD.A’B’C’D’ là.

• Cho khối chóp S.ABC có SA vuông góc với đáy, SA=4, AB=6, BC=10 và CA=8. Tính thể tích V của khối chóp S.ABC.

• Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân đỉnh B, AB = 4,SA = SB = SC = 12 . Gọi M, N, E lần lượt là trung điểm AC, BC, AB. Trên cạnh SB lấy điểm F sao cho \( \frac{{BF}}{{BS}} = \frac{2}{3}\) Thể tích khối tứ diện (MNEF ) bằng

• Cho \(\left( H \right)\) là khối lập phương có độ dài cạnh bằng \(3\left( {cm} \right)\). Thể tích của \(\left( H \right)\) bằng

• Cho hình lập phương ABCD.A'B'C'D' có đường chéo bằng \(a\sqrt 3 \). Tính thể tích khối chóp A'.ABCD.

• Cho hình chóp S ABC . có đáy là tam giác vuông cân tại C, AB = 3. Hình chiếu vuông góc của S xuống mặt đáy trùng với trọng tâm của tam giác ABC và \(S B=\frac{\sqrt{14}}{2}\). Thể tích của khối chóp đã cho bằng
   

• Thể tích V của khối lăng trụ có diện tích đáy bằng 3 và độ dài đường cao bằng 4 là

• Cho khối lăng trụ có diện tích đáy bằng a² và khoảng cách giữa hai đáy bằng 3a. Tính thể tích V của khối lăng trụ đã cho.

• Cho hình chóp tứ giác đều S.ABCD, cạnh đáy là a, SA = 2a. Thể tích khối chóp là:

• Cho khối chóp S ABC . có đáy là tam giác vuông tại B, \(A B=a, \quad A C=2 a\)2 . Cạnh bên SA vuông góc với mặt phẳng đáy và S A=a. Thể tích của khối chóp đã cho bằng

• Cho hình lăng trụ tam giác đều có cạnh đáy và cạnh bên đều bằng a. Gọi S là diện tích xung quanh của hình lăng trụ trên. Tính S.