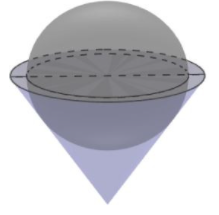
Cho lăng trụ đứng \(ABC.A'B'C'\) có đáy là tam giác đều cạnh \(a\). Mặt phẳng \(\left( AB'C' \right)\) tạo với mặt đáy góc \({{60}^{0}}\) và điểm \(G\) là trọng tâm tam giác \(ABC\). Bán kính mặt cầu ngoại tiếp khối chóp \(G.A'B'C'\) bằng:
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiGọi \(M\) là trung điểm \(B'C'\), ta có
\({{60}^{0}}=\widehat{\left( AB'C' \right),\left( A'B'C' \right)}=\widehat{AM,A'M}=\widehat{AMA'}\).
Trong \(\Delta AA'M\), có \(A'M=\frac{a\sqrt{3}}{2}\);
\(AA'=A'M.\tan \widehat{AMA'}=\frac{3a}{2}\).
Gọi \(G'\) là trọng tâm tam giác đều \(A'B'C'\), suy ra \(G'\) cũng là tâm đường tròn ngoại tiếp \(\Delta A'B'C'.\)
Vì lặng trụ đứng nên \(GG'\bot \left( A'B'C' \right)\).
Do đó \(GG'\) là trục của tam giác \(A'B'C'\).
Trong mặt phẳng \(\left( GC'G' \right)\), kẻ trung trực \(d\) của đoạn thẳng \(GC'\) cắt \(GG'\) tại \(I\). Khi đó \(I\) là tâm mặt cầu ngoại tiếp khối chóp \(G.A'B'C'\), bán kính \(R=GI.\)
Ta có \(\Delta GPI\,\,\ddot{y}\,\,\Delta GG'C'\Rightarrow \frac{GP}{GI}=\frac{GG'}{GC'}\)
\(\Rightarrow R=GI=\frac{GP.GC'}{GG'}=\frac{GC{{'}^{2}}}{2GG'}=\frac{GG{{'}^{2}}+G'C{{'}^{2}}}{2GG'}=\frac{31a}{36}\).
Câu hỏi liên quan
-
Cho tứ diện đều ABCD có cạnh a. Một mặt cầu tiếp xúc với các mặt của tứ diện có bán kính là:
-
Người ta thả một viên bi sắt có dạng hình cầu với bán kính nhỏ hơn 4,5cm vào một chiếc cốc hình trụ đang chứa nước thì viên bi sắt đó tiếp xúc với đáy cốc và tiếp xúc với mặt nước sau khi dâng (tham khảo hình vẽ bên). Biết rằng bán kính của phần trong đáy cốc bằng 5,4cm và chiều cao của mực nước ban đầu trong lòng cốc bằng 4,5cm. Bán kính của viên bi sắt đó bằng:
-
Trong không gian Oxyz, mặt cầu \(\left( S \right)\) có tâm là điểm \(I\left( {1\,;\, – 1\,;\,2} \right)\) và cắt mặt phẳng \(\left( P \right):2x – 2y + z + 3 = 0\) theo một đường tròn có bán kính bằng 4 có phương trình là
-
Trong mặt phẳng tọa độ Oxyz, cho bốn điểm \(A\left( {0; – 1;2} \right), B\left( {2; – 3;0} \right), C\left( { – 2;1;1} \right), D\left( {0; – 1;3} \right)\). Gọi \(\left( L \right)\) là tập hợp tất cả các điểm M trong không gian thỏa mãn \(\overrightarrow {MA} .\overrightarrow {MB} = \overrightarrow {MC} .\overrightarrow {MD} = 1\). Biết rằng \(\left( L \right)\) là một đường tròn, đường tròn đó có bán kính r bằng bao nhiêu?
-
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\), hình chiếu vuông góc của đỉnh \(S\) trên mặt phẳng \(\left( ABC \right)\) là trung điểm \(H\) của cạnh \(BC\). Góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( ABC \right)\) bằng \({{60}^{0}}\). Gọi \(G\) là trọng tâm tam giác \(SAC\), \(R\) là bán kính mặt cầu có tâm \(G\) và tiếp xúc với mặt phẳng \(\left( SAB \right)\). Đẳng thức nào sau đây sai?
-
Trong không gian mặt cầu có tâm là gốc tọa độ \(O\left( {0;0;0} \right)\) và đi qua điểm \(M\left( {0;0;2} \right)\) có phương trình là
-
Công thức tính bán kính mặt cầu ngoại tiếp hình chóp có cạnh bên vuông góc với đáy là:
-
Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng \((P): 2 x+2 y-z-3=0 \text { và điểm } I(1 ; 2-3)\) . Mặt cầu (S) tâm I và tiếp xúc mp(P) có phương trình:
-
Trong không gian với hệ toạ độ Oxyz, cho mặt cầu \(\left( S \right):\,{\left( {x – 1} \right)^2} + {\left( {y – 3} \right)^2} + {\left( {z – 2} \right)^2} = 4\). Gọi \(N\left( {{x_0};{y_0};{z_0}} \right)\) là điểm thuộc \(\left( S \right)\) sao cho khoảng cách từ điểm N đến mặt phẳng \(\left( {Oxz} \right)\) lớn nhất. Giá trị của biểu thức \(P = {x_0} + {y_0} + {z_0}\) bằng
-
Trong không gian Oxyz, cho hai mặt cầu \(\left( {{S_1}} \right):\,{x^2} + {\left( {y + 2} \right)^2} + {\left( {z – 2} \right)^2} = 25, \left( {{S_2}} \right):\,{x^2} + {y^2} + {z^2} – 2y + 4z – 4 = 0\). Biết các tiếp tuyến chung của hai mặt cầu đồng phẳng với đường thẳng nối tâm của hai mặt cầu đi qua điểm cố định \(M\left( {a;b;c} \right)\). Tính \({a^2} + bc\) bằng
-
Để tính diện tích xung quanh của một khối cầu bằng đá, người ta thả nó vào một chiếc thùng hình trụ có chiều cao 2m, bán kính đường tròn đáy 0,5m và có chứa sẵn một lượng nước có thể tích bằng 1/8 thể tích của thùng. Sau khi thả khối cầu bằng đá vào, người ta đo được mực nước trong thùng cao gấp 3 lần mực nước ban đầu khi chưa thả khối cầu bằng đá vào. Diện tích xung quanh của khối cầu bằng đá gần nhất với kết quả nào dưới đây ?
-
Một bình đựng nước dạng hình nón (không có đáy), đựng đầy nước. Người ta thả vào đó một khối cầu có đường kính bằng chiều cao của bình nước và đo được thể tích nước tràn ra ngoài là 18π(dm3) . Biết rằng khối cầu tiếp xúc với tất cả các đường sinh của hình nón và đúng một nửa của khối cầu chìm trong nước (hình bên). Tính thể tích V của nước còn lại trong bình.
-
Thể tích của khối cầu có bán kính 3a bằng
-
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu \(\left( S \right):\,\,{\left( {x – 2} \right)^2} + {\left( {y – 3} \right)^2} + {\left( {z – 5} \right)^2} = 9\) và tam giác ABC với \(A(5;0;0),\,\,B(0;3;0),\,\,C(4;5;0)\). Tìm tọa độ điểm M thuộc cầu (S) sao cho khối tứ diên MABC có thể tích lớn nhất.
-
Trong không gian với hệ tọa độ Oxyz , cho mặt cầu (S) có phương trình \(x^{2}+y^{2}+z^{2}+2 x-6 y+1=0\) . Tính tọa độ tâm I , bán kính R của mặt cầu (S).
-
Cho mặt cầu S(O;R) và mặt phẳng (α). Biết khoảng cách từ O tới (α) bằng d. Nếu d < R thì giao tuyến của mặt phẳng (α) với mặt cầu S(O;R) là đường tròn có bán kính bằng bao nhiêu?
-
Mặt cầu (S) có tâm \(I(1 ; 2 ;-1) \) và tiếp xúc với mặt phẳng \((P): x-2 y-2 z-8=0\) có phương trình là
-
Một mặt cầu có bán kính bằng a. Diện tích của mặt cầu đó là:
-
Cho mặt cầu (S) tâm O bán kính R và một mặt phẳng (P). Kí hiệu h là khoảng cách từ O đến mặt phẳng (P). Mặt phẳng (P) có nhiều hơn một điểm chung với mặt cầu (S) nếu:
-
Trong không gian hệ tọa độ Oxyz cho mặt cầu \(\left( S \right):{x^2} + {y^2} + {x^2} - 2x + 2y - 4z - 10 = 0\) và mặt phẳng (P): :2x + y - z - 5 = 0. Viết phương trình mặt phẳng (Q) song song với mặt phẳng (P) và cắt mặt cầu (S) theo đường tròn có bán kính bằng một nửa bán kính mặt cầu (S):
