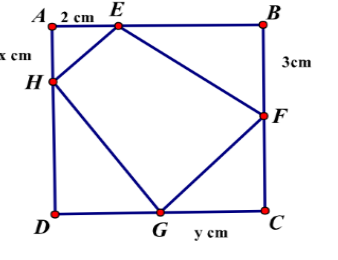
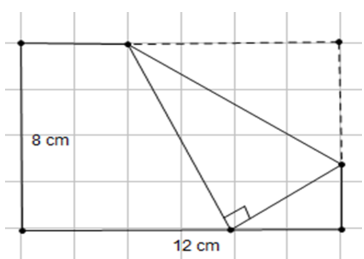
Cho một tờ giấy hình chữ nhật với chiều dài 12 cm và chiều rộng 8 cm. Gấp góc bên phải của tờ giấy sao cho góc ở đỉnh của nó chạm với đáy như hình vẽ. Khi độ dài nếp gấp là nhỏ nhất thì giá trị nhỏ nhất đó là bao nhiêu.
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo sai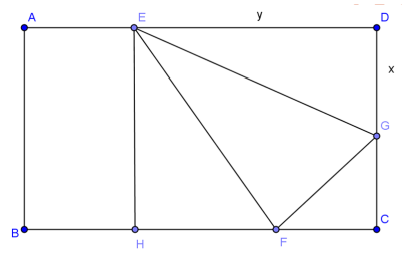
Đặt DG=FG=x,ED=HC=EF=y. Khi đó
FC=√x2−(8−x)2=√16x−64,HF=y−√16x−64
Ta có
EF=√82+(y−√16x−64)2=y⇔64+y2−2y√16x−64+16x−64=y2⇔y=8√16x−64x
Độ dài nếp gấp là f(x)=x+y=x+8√16x−64x với 0<x<8
ta thấy với x=6√3 thì f(x) nhỏ nhất.
ADMICRO
YOMEDIA
ZUNIA9
.PNG)
.jpg.png)