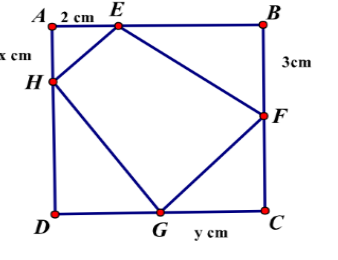
Cho một tấm nhôm hình vuông cạnh 6 cm. Người ta muốn cắt một hình thang như hình vẽ. Tìm tổng x + y để diện tích hình thang EFGH đạt giá trị nhỏ nhất.

Cho hàm số \(y = \frac{{x + m}}{{x + 1}}\) (m là tham số thực) thoả mãn \(\mathop {\min }\limits_{\left[ {1\;;\;2} \right]} y + \mathop {{\rm{max}}}\limits_{\left[ {1\;;\;2} \right]} y = \frac{{16}}{3}\). Mệnh đề nào dưới đây đúng?

Gọi \(M,\,m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( x \right) = \frac{{x + 1}}{{x – 1}}\) trên đoạn \(\left[ {3;\,5} \right]\). Khi đó M – m bằng

Tìm giá trị lớn nhất của hàm số \(f(x)=\left|x^{3}+3 x^{2}-72 x+90\right| \text { trên }[-5 ; 5]\)

Trong số các hình chữ nhật có cùng chu vi 16 cm, hình chữ nhật có diện tích lớn nhất bằng:

Hàm số \(y=x^{8}+\left(x^{4}-1\right)^{2}\) đạt giá trị lớn nhất, giá trị nhỏ nhất trên đoạn [1;2] lần lượt tại hai điểm có hoành độ \(x_{1} ; x_{2}\). Khi đó tích \(x_{1} . x_{2}\) có giá trị bằng
 

Giá trị nhỏ nhất của hàm số \(y = {e^x}\) trên đoạn \(\left[ { – 1;\,\,1} \right]\) là:

Hàm số \(y=\sqrt{x^{2}+1}+x^{2}\) có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn [-1;1] lần lượt là:

Cho hình vẽ

Bạn An có một tấm nhôm hình chữ nhật có chiều dài 12(m), chiều rộng 6(m). Bạn nhờ bác thợ hàn cắt ở bốn góc bốn hình vuông bằng nhau và gập tấm nhôm lại (như hình trên) để được một cái hộp không nắp dùng để đựng nước. Hỏi bác thợ hàn phải cắt cạnh hình vuông bằng bao nhiêu sao cho khối hộp chứa được nhiều nước nhất ?

Gọi S là tập hợp tất cả các giá trị của tham số m để hàm số \(y=\left|x^{2}+x+m\right|\) thỏa mãn \(\min\limits _{[-2 ; 2]} y=2\) . Tổng tất cả các phần tử của S bằng
 

Cho hàm số có f(x) có đạo hàm là hàm \(f^{\prime}(x)\). Đồ thị hàm số \(f^{\prime}(x)\) như hình vẽ bên. Biết rằng \(f(0)+f(1)-2 f(2)=f(4)-f(3)\) . Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của f(x) trên đoạn [0;4]?

Giá trị nhỏ nhất của hàm số \(y=\sqrt{x+1}\) là:

Đồ thị hàm số \(y = f’\left( x \right)\) là đường cong nét đậm và \(y = g’\left( x \right)\) là đường cong nét mảnh như hình vẽ. Gọi ba giao điểm A,B,C của \(y = f’\left( x \right)\) và \(y = g’\left( x \right)\) trên hình vẽ lần lượt có hoành độ a,b,c. Tìm giá trị nhỏ nhất của hàm số \(h\left( x \right) = f\left( x \right) – g\left( x \right)\) trên đoạn \(\left[ {a;c} \right]\)?

Giá trị lớn nhất của hàm số f\(f(x)=x \cdot e^{-2 x}\) trên đoạn [ 0;1] bằng

Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số \(y=\sin ^{20} x+\cos ^{20} x\) . Khi đó M.m bằng
 

Giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = {x^3} + 2{x^2} – 4x + 3\) trên đoạn \(\left[ { – 4;0} \right]\) lần lượt là \(M{\rm{ và }}m\). Giá trị của tổng M + m bằng bao nhiêu?

Cho hàm số y = f( x) đạo hàm f’ (x) = -x²- 1. Với các số thực dương a, b thỏa mãn a < b. Giá trị nhỏ nhất của hàm số f( x) trên đoạn [ a; b] bằng

Tìm GTLN và GTNN của hàm số \(y = {x^5} – 5{x^4} + 5{x^3} + 1\) trên \(\left[ { – 1;2} \right]?\)

Cho hàm số \(y = f\left( x \right)\) có đồ thị hàm số \(y = f’\left( x \right)\) như hình vẽ

Đặt \(g\left( x \right) = \frac{1}{3}{x^3} – x – f\left( x \right) + 2020\). Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(g\left( x \right)\) trên đoạn \(\left[ { – \sqrt 3 ;\,\sqrt 3 } \right]\). Hãy tính M + m.

Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right)\). Hàm số \(y = f’\left( x \right)\) liên tục trên tập số thực và có đồ thị như hình vẽ.

Biết \(f\left( { – 1} \right) = \frac{{13}}{4},\,f\left( 2 \right) = 6\). Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(g\left( x \right) = {f^3}\left( x \right) – 3f\left( x \right)\) trên \(\left[ { – 1;2} \right]\) bằng

Hàm số \(y=(x-1)(x-2)(x-3)(x-4)\) có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn [-1;3] là: