Hàm số \(y=\frac{1}{x}+\frac{1}{x+1}+\frac{1}{x+2}\) đạt giá trị lớn nhất trên đoạn [- 5; -3] bằng:
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo sai\(\begin{aligned} &\mathrm{TXĐ}: D=\mathbb{R} \backslash\{-2 ;-1 ; 0\}\\ &\text { Ta có: } \quad y^{\prime}=-\frac{1}{x^{2}}-\frac{1}{(x+1)^{2}}-\frac{1}{(x+2)^{2}}<0 ; \forall x \in D \end{aligned}\)
Bảng biến thiên
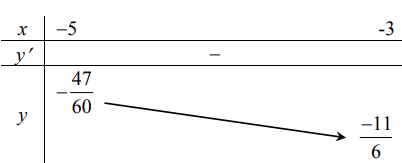
Từ BBT ta thấy, hàm số có giá trị lớn nhất bằng \(-\frac{47}{60}\)
ADMICRO
YOMEDIA
ZUNIA9
.jpg.png)
.jpg.png)
.PNG)











