Gọi S là tập hợp tất cả các giá trị của tham số m để hàm số \(y=\left|x^{2}+x+m\right|\) thỏa mãn \(\min\limits _{[-2 ; 2]} y=2\) . Tổng tất cả các phần tử của S bằng
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
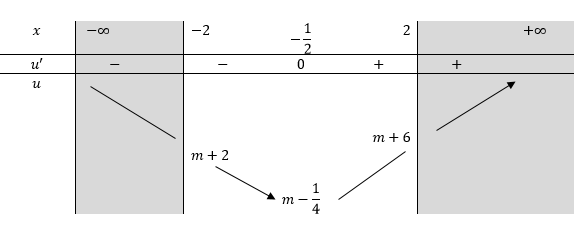
Báo sai\(\text { Xét hàm số } u=x^{2}+x+m \text { trên đoạn }[-2 ; 2], \text { có: } u^{\prime}=0 \Leftrightarrow 2 x+1=0 \Leftrightarrow x=-\frac{1}{2} \text { . }\)
\(\max \limits_{[-2 ; 2]} u=\max \left\{u(-2), u\left(-\frac{1}{2}\right), u(2)\right\}=m+6\)
\(\min\limits _{[-3 ; 2]} u=\min \left\{u(-2), u\left(-\frac{1}{2}\right), u(2)\right\}=m-\frac{1}{4}\)
\(\text { Nếu } m-\frac{1}{4} \geq 0 \text { hay } m \geq \frac{1}{4} \text { thì } \min _{[-2 ; 2]} y=m-\frac{1}{4}=2 \Leftrightarrow m=\frac{9}{4} \text { (thỏa mãn). }\)
\(\text { Nếu } m+6 \leq 0 \text { hay } m \leq-6 \text { thì } \min _{[-2 ; 2]} y=-m-6=2 \Leftrightarrow m=-8 \text { (thỏa mãn). }\)
\(\text { Nếu }-6<m<\frac{1}{4} \text { thì } \min _{[-2 ; 2]} y=0 \text { (không thỏa mãn). }\)
\(\text { Ta có: } S=\left\{-8 ; \frac{9}{8}\right\} \text { . }\)
Vậy tổng các phần tử của S là \(\begin{equation} -\frac{23}{4} \end{equation}\)
.png)
.jpg.png)
.jpg.png)
.jpg.png)











