Mặt cầu (S) tâm I(2; 3; −1) cắt đường thẳng \(d:\,\frac{{x - 11}}{2} = \frac{y}{1} = \frac{{z + 25}}{{ - 2}}\) tại 2 điểm A, B sao cho AB = 16 có bán kính là:
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai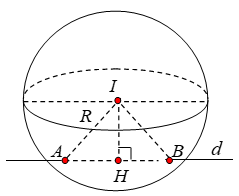
Đường thẳng d đi qua M(11;0;-25) và có vectơ chỉ phương \(\overrightarrow u = \left( {2;1; - 2} \right),\overrightarrow {MI} = \left( { - 9;3;24} \right),\left[ {\overrightarrow u ,\overrightarrow {MI} } \right] = \left( {30; - 30;15} \right)\)
Gọi H là hình chiếu của I trên (d). Ta có:
\(\begin{array}{l}
IH = d\left( {I,AB} \right) = \frac{{\left| {\left[ {\overrightarrow u ,\overrightarrow {MI} } \right]} \right|}}{{\left| {\overrightarrow u } \right|}} = \frac{{\sqrt {{{30}^2} + {{\left( { - 30} \right)}^2} + {{15}^2}} }}{{\sqrt {{2^2} + {1^2} + {{\left( { - 2} \right)}^2}} }} = 15\\
\Rightarrow R = \sqrt {I{H^2} + H{B^2}} = \sqrt {{{15}^2} + {8^2}} = 17
\end{array}\)











