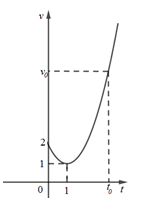
Một chất điểm A xuất phát từ O, chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật \(v(t)=\frac{1}{120} t^{2}+\frac{58}{45} t(\mathrm{~m} / \mathrm{s})\) , trong đó t (giây) là khoảng thời gian tính từ lúc A bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm B cũng xuất phát từ O, chuyển động thẳng cùng hướng với A nhưng chậm hơn 3 giây so với A và có gia tốc bằng \(a\left(\mathrm{~m} / \mathrm{s}^{2}\right)\) (a là hằng số). Sau khi B xuất phát được 15 giây thì đuổi kịp A . Vận tốc của B tại thời điểm đuổi kip A bằn
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTừ đề bài, ta suy ra: tính từ lúc chất điểm A bắt đầu chuyển động cho đến khi bị chất điểm B bắt kịp thì A đi được 18 giây, B đi được 15 giây.
Biểu thức vận tốc của chất điểm B có dạng \(v_{B}(t)=\int a \mathrm{~d} t=a t+C \text { , lại có } v_{B}(0)=0 \text { nên }\) \(v_{B}(t)=a t .\)
Từ lúc chất điểm A bắt đầu chuyển động cho đến khi bị chất điểm B bắt kịp thì quãng đường hai chất điểm đi được là bằng nhau. Do đó
\(\int_{0}^{18}\left(\frac{1}{120} t^{2}+\frac{58}{45} t\right) \mathrm{d} t=\int_{0}^{15} a t \mathrm{~d} t \Leftrightarrow 225=\frac{225}{2} a \Leftrightarrow a=2\)
Từ đó, vận tốc của B tại thời điểm đuổi kịp A bằng \(v_{B}(15)=2.15=30(\mathrm{~m} / \mathrm{s})\)
Câu hỏi liên quan
-
Gọi h(t) (cm) là mức nước ở bồn chứa sau khi bơm nước được t giây. Biết rằng \(h'(t) = \frac{1}{5}\sqrt[3]{{t + 8}}dt\) và lúc đầu bồn không có nước. Mức nước ở bồn sau khi bơm nước được 6 giây xấp xỉ bằng:
-
Diện tích của hình phẳng được giới hạn bởi các đường \(\displaystyle y = \tan x,y = 0,x = - \frac{\pi }{4}\) và \(\displaystyle x = \frac{\pi }{4}\) bằng
-
Một vật chuyển động trong 4 giờ với vận tốc v (km/h) phụ thuộc vào thời gian t ,(h) có đồ thị là một phần của đường parabol có đỉnh I(1;1) và trục đối xứng song song với trục tung như hình bên. Tính quãng đường s mà vật di chuyển được trong 4 giờ kể từ lúc xuất phát
-
Trên mặt phẳng Oxy, cho hình phẳng ( ) H giới hạn bởi các đường \(\begin{aligned} &(P): y=x^{2},\left(P^{\prime}\right): y=4 x^{2} \text { và } \text { (d): } y=4 \end{aligned}\) . Thể tích của khối tròn xoay khi quay (H ) quanh trục
Ox bằng -
Tính diện tích hình phẳng giới hạn bởi đồ thị các hàm số \(y = {x^2} - 4\), \(y = - {x^2} - 2x\) và đường thẳng \(x = - 3,x = - 2\)
-
Cho hình phẳng (H) giới hạn bởi đồ thị hàm số \(y=\frac{1}{x}\), trục Ox và hai đường thẳng \(x=1, x=2\). Khối tròn xoay tạo thành khi quay hình phẳng (H) quanh trục Ox có thể tích là
-
Cho nửa đường tròn đường kính (\(AB=4\sqrt5\) ). Trên đó người ta vẽ một parabol có đỉnh trùng với tâm của nửa hình tròn, trục đối xứng là đường kính vuông góc với AB. Parabol cắt nửa đường tròn tại hai điểm cách nhau 4cm và khoảng cách từ hai điểm đó đến AB bằng nhau và bằng 4cm. Sau đó người ta cắt bỏ phần hình phẳng giới hạn bởi đường tròn và parabol (phần gạch chéo trong hình vẽ). Đem phần còn lại quay xung quanh trục AB. Thể tích của khối tròn xoay thu được bằng:
-
Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f( x ) = x^2 - 1\), trục hoành và hai đường thẳng x = - 1; x = - 3 là:
-
Cho hàm số \(y=(x-2)^{2}\) có đồ thị (C) , khối tròn xoay tạo thành khi quay hình phẳng giới
hạn bởi (C) , trục Ox , trục Oy và đường thẳng x = 3 có thể tích là -
Diện tích hình phẳng giới hạn bởi hai đường thẳng \(x=0 , x=\pi \) đồ thị hàm số y=cos x và trục Ox là
-
Tính diện tích hình phẳng giới hạn bởi các đường sau:
\(\displaystyle y = {x^3} - {x^2}\) và \(\displaystyle y = \frac{1}{9}(x - 1)\)
-
Cho hai hàm số f( x ) = - x và g( x ) = ex. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số y = f( x ),y = g( x ) và hai đường thẳng x = 0,x = e là:
-
Cho hình phẳng giới hạn (H) như hình vẽ bên. Thể tích khối tròn xoay sinh ra khi quay hình phẳng (H) quanh trục Oy là
-
Diện tích của hình phẳng giới hạn bởi các đường \(\displaystyle {y_1} = {x^3};{y_2} = 4x\) bằng
-
Cho hàm số y=f( x ) liên tục trên đoạn [ a;b ]. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y=f( x ), trục hoành và hai đường thẳng x=a,x=b ( a<b ). Thể tích của khối của khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức:
-
Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = \sqrt x ,y = 6 - x\) và trục hoành.
-
Quay hình phẳng G giới hạn bởi các đường y=x3,y=1,x=0 xung quanh trục Oy. Khi đó thể tích của khối tròn xoay này bằng:
-
Cho hàm số y=f(x) liên tục trên [ a;b ]. Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y=f(x), trục hoành và hai đường thẳng (x=a; x=b) được tính theo công thức
-
Một tập đoàn định đầu tư vào hai dự án. Giả sử, dự án đầu tư đầu có tốc độ sinh lợi nhuận là \(P_{1}(t)=50+t^{2}(\text { đồng/năm) }\), dự án thứ hai có tốc độ sinh lợi nhuận là \(P_{2}(t)=200+5 t(\text { đồng/năm) }\). Sau t năm thì tốc độ sinh lợi của dự án hai bằng một nửa dự án một. Tính lợi nhuận thực tế trong khoảng thời gian trên.
-
Cho hình phẳng B giới hạn bởi các đường \(x = \sqrt 5 {y^2},x = 0,y = - 1\) và \(y = 1\). Tính thể tích của khối tròn xoay tạo thành khi quay hình B quanh trục tung.
