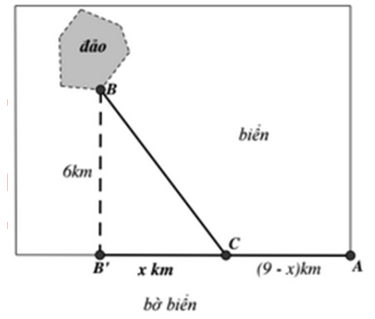
Một công ty muốn làm đường ống dẫn từ một điểm A trên bờ đến một điểm B trên một hòn đảo. Hòn đảo cách bờ biển 6 km . Giá để xây đường ống trên bờ là 50000 USD mỗi km , và 130000 USD mỗi km để xây dưới nước. B' là điểm trên bờ biển sao cho BB' vuông góc với bờ biển. Khoảng cách từ A đến B' là 9 km . Vị trí C trên đoạn AB' sao cho khi nối ống theo ACB thì số tiền ít nhất. Khi đó C cách A một đoạn bằng bao nhiêu ?

 

Câu hỏi liên quan

• Giá trị lớn nhất M, giá trị nhỏ nhất m của hàm số $y=\sin ^{4} x-4 \sin ^{2} x+5$ là:

• Giá trị lớn nhất của hàm số y = x³ – 3x + 1 trên [0; 1] là:

• Hàm số $y=-2 \sin ^{3} x+3 \cos 2 x-6 \sin x+4$ có giá trị lớn nhất bằng

ZUNIA12

• Hàm số $y = \frac{{{x^2} - 3x}}{{x + 1}}$ có giá trị lớn nhất trên đoạn [0;3] là

• GTLN của hàm số y = 2sinx + cos2x trên đoạn [0; π] là

• Hàm số $y = \sqrt {1 - x}  + \sqrt {x + 3}  + \sqrt {1 - x} .\sqrt {x + 3}$ có giá trị lớn nhất, giá trị nhỏ nhất là:

• Gọi giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f(x) = \frac{{{x^2} – 3{\rm{x}} + 6}}{{x – 1}}$ trên đoạn $\left[ {2;4} \right]$ lần lượt là $M,\,\,m$. Tính $S = M + \,\,m.$

• Tìm hai số có hiệu là 13 sao cho tích của chúng là bé nhất.

•  

  Cho hàm số y =f(x) liên tục trên $\left[0 ; \frac{7}{2}\right]$ có đồ thị hàm số y=f'(x) như hình vẽ sau: 

  

  Hàm số y=f(x) đạt giá trị nhỏ nhất trên $\left[0 ; \frac{7}{2}\right]$ tại điểm x₀ nào dưới đây?
   

• Cho hàm số $y = \frac{{x + m}}{{x - 1}}$ với tham số m bằng bao nhiêu thì min_[2;4] y = 3

• Hàm số $y=\sin ^{4} x-\cos ^{4} x$ có giá trị lớn nhất bằng:

• Giá trị nhỏ nhất của hàm số $y = \sqrt {6 - x}  - \sqrt {x + 4}$ đạt tại x₀, tìm x₀?

• Cho hàm số $y=\frac{x^{2}-3}{x-2}$. Khẳng định nào sau đây đúng về giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn [3 ; 4]:

• Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có bảng biến thiên trên đoạn $\left[ { – 1;4} \right]$ như sau:

  

  Giá trị lớn nhất của hàm số $y = \left| {f\left( x \right)} \right|$ trên đoạn đoạn $\left[ { – 1;4} \right]$ bằng

• Tìm x để hàm số $y=x+\sqrt{4-x^{2}}$ đạt giá trị lớn nhất. 

• Giá trị nhỏ nhất của hàm số $y=5 \sin x-\cos 2 x$ là:

• Có tất cả bao nhiêu giá trị của tham số m để giá trị lớn nhất của hàm số $y = \left| {{x^2} – 2x + m} \right|$ trên đoạn $\left[ { – 1;2} \right]$ bằng 5.

• Giá trị nhỏ nhất của hàm số $y = – {x^4} + 4{x^2} – 5$ trên đoạn $\left[ { – 2;3} \right]$ bằng

• Hàm số $y=\frac{x^{2}-2}{\sqrt{x^{2}+1}}$ có giá trị nhỏ nhất tại điểm có hoành độ bằng:

• Hàm số $y=\sqrt{3} \sin x+\cos x$ có giá trị lớn nhất, giá trị nhỏ nhất lần lượt là: