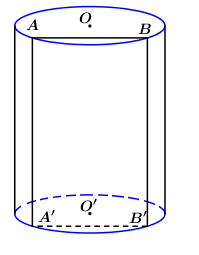
Một hình trụ có diện tích xung quanh là (\(16\pi \)), thiết diện qua trục là hình vuông. Một mặt phẳng ( \(\alpha \)) song song với trục, cắt hình trụ theo thiết diện là (ABB'A' ), biết một cạnh thiết diện là một dây của đường tròn đáy hình trụ và căng một cung 1200. Chu vi tứ giác (ABB'A' ) bằng:
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiGọi r,h lần lượt là bán kính đáy và chiều cao của hình trụ, ta có \( {S_{xq}} = 2\pi rh \Leftrightarrow 16\pi = 2\pi rh \Leftrightarrow rh = 8\)
Lại có thiết diện qua trục là hình vuông nên h=2r, do đó
\( r.2r = 8 \Leftrightarrow {r^2} = 4 \Rightarrow r = 2,{\mkern 1mu} {\mkern 1mu} h = 4 = AA'\)
Theo bài ra ta có: ∠AOB=1200
Áp dụng định lí Cosin trong tam giác OAB ta có:
\(\begin{array}{l} \begin{array}{*{20}{l}} {A{B^2} = O{A^2} + O{B^2} - 2.OA.OB.\cos \angle AOB}\\ {A{B^2} = {r^2} + {r^2} - 2.r.r.\cos {{120}^0}}\\ {A{B^2} = 3{r^2}}\\ { \Rightarrow AB = r\sqrt 3 = 2.\sqrt 3 } \end{array}\\ \to {C_{ABB'A'}} = 2\left( {AB + AA'} \right) = 2\left( {2\sqrt 3 + 4} \right) = 8 + 4\sqrt 3 \end{array}\)