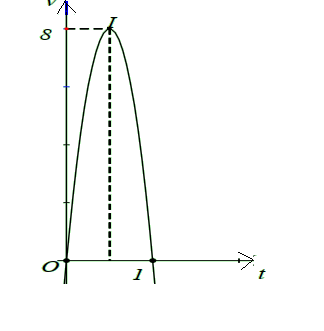
Một người chạy trong 1 giờ với vận tốc v(km/h) phụ thuộc thời gian t (h) có đồ thị của vận tốc là một phần của đường parabol có đỉnh \(I\left(\frac{1}{2} ; 8\right)\) và trục đối xứng song song với trục tung như hình vẽ bên. Tính quãng đường s mà người đó chạy được trong khoảng thời gian 45 phút, kể từ khi bắt đầu chạy 

Cho hình (H) giới hạn bởi đường cong \(x = \sqrt y \), trục tung và hai đường thẳng y = 1,y = 4  Thể tích khối tròn xoay tạo thành khi quay (H) quanh trục Oy được tính theo công thức

Một đám vi khuẩn tại ngày thứ x có số lượng là N(x). Biết rằng N'(x) = \(\frac{{2000}}{{1 + x}}\) và lúc đầu số lượng vi khuẩn là 5000 con. Vậy ngày thứ 12 số lượng vi khuẩn (sau khi làm tròn) là bao nhiêu con?

Tính thể tích khối tròn xoay khi quay hình phẳng xác định bởi: \(\displaystyle  y = 2 - {x^2},y = 1\), quanh trục \(\displaystyle  Ox\).

Cho hàm số y=f(x) liên tục trên [ a;b ]. Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y=f(x), trục hoành và hai đường thẳng (x=a; x=b) được tính theo công thức

Thể tích vật thể tròn xoay sinh ra khi quay hình phẳng giới hạn bới các đường \(x=\sqrt y; ,y=-x+2,x=0 \) quanh trục Ox có giá trị là kết quả nào sau đây ?

Một xe lửa chuyển động chậm dần đều và dừng hẳn sau 20 giây kể từ khi bắt đầu hãm phanh. Trong thời gian đó xe chạy được 120m . Cho biết công thức vận tốc của chuyển động biến đổi đều là \(v(t)=v_{0}+a t(\mathrm{~m} / \mathrm{s})\) , trong đó \(a\left(\mathrm{~m} / \mathrm{s}^{2}\right)\) là gia tốc và v(m/s) là vận tốc tại thời điểm t(s ) . Hãy tính vận tốc v₀ lúc bắt đầu hãm phanh 

Tính diện tích của hình phẳng giới hạn bởi đồ thị hàm số \(y = - {x^2}\), trục hoành, và hai đường thẳng \(x = - 1;x = 2\).

Một ô tô bắt đầu chuyển động nhanh dần đều với gia tốc \(a_{1}=7\left(m / s^{2}\right)\). Đi được 5s , tài xế phát hiện chướng ngại vật phía trước và phanh gấp, sáu đó ô tô chuyển động chậm dần đều với gia tốc \(a_{2}=-70\left(\mathrm{~m} / \mathrm{s}^{2}\right) \text { . }\)Tính quãng đường đi được của ô tô từ lúc bắt đầu chuyển động cho đến khi dừng hẳn. 

Hình phẳng giới hạn bởi đồ thị hàm số \(y=f( x ) \) liên tục trên đoạn [ 1; 3 ], trục Ox và hai đường thẳng (x=1, x=3 ) có diện tích là:

Cho hàm số y=f(x) liên tục trên đoạn ( a;b )và \(f(x)>0, \forall x \in (a;b )\). Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y=f(x), trục hoành và 2 đường thẳng x=a, x=b ,(a<b). Thể tích của vật thể tròn xoay khi quay D quanh Ox được tính theo công thức:

Một vật chuyển động với vận tốc \(v\left( t \right) = 1,2 + \frac{{{t^2} + 4}}{{t + 3}}\left( {m/s} \right).\) Quãng đường vật đi được sau 4s xấp xỉ bằng:

Cho hình phẳng giới hạn (H) như hình vẽ bên. Thể tích khối tròn xoay sinh ra khi quay hình phẳng (H) quanh trục Ox là

Một chất điểm A xuất phát từ O, chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật \(v(t)=\frac{1}{180} t^{2}+\frac{11}{18} t(\mathrm{~m} / \mathrm{s})\), trong đó t (giây) là khoảng thời gian tính từ lúc A bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm B cũng xuất phát từ O, chuyển động thẳng cùng hướng với A nhưng chậm hơn 5 giây so với A và có gia tốc bằng \(a\left(\mathrm{~m} / \mathrm{s}^{2}\right)\) (a là hằng số). Sau khi B xuất phát được 10 giây thì đuổi kịp A . Vận tốc của B tại thời điểm đuổi kip A bằn 

Một vật bắt đầu chuyển động với vận tốc đầu là 6(m/s) và có gia tốc được cho bởi công thức \(a(t)=v^{\prime}(t)=\frac{3}{t+1}\left(m / s^{2}\right) .\) Vận tốc của vật sau 8 giây là \(v(8)=a \ln 3+b(a, b \in \mathbb{Z}), \text { tính } P=a-b \text { . }\)

Cho hình phẳng (H) giới hạn bởi đồ thị hàm số \(y = x^3 - 4x \), trục hoành, đường thẳng x =  - 2 và đường thẳng x = 1. Diện tích của hình phẳng ( H) bằng

Vận tốc của một vật chuyển động là \(v\left( t \right)\; = \;\frac{1}{{2{\rm{\pi }}}}\; + \;\frac{{\sin \left( {{\rm{\pi }}t} \right)\;}}{{\rm{\pi }}}\) (m/s). Quãng đường vật di chuyển trong khoảng thời gian 1,5 giây xấp xỉ bằng:

Tính thể tích vật thể có đáy là một hình tròn giới hạn bởi \(\displaystyle  {x^2} + {y^2} = 1\). Mỗi thiết diện vuông góc với trục \(\displaystyle  Ox\) là một hình vuông.

Cho hình phẳng \(A\) giới hạn bởi các đường \(y = 0, x = 4\), và \(y = \sqrt x  - 1\). Tính thể tích của khối tròn xoay tạo thành khi quay hình \(A\) quanh trục hoành.

Một vật chuyển động với vận tốc \(v(t)=1-2 \sin 2 t(m / s) . \text { Gọi } S=a+\frac{b \pi}{c}(a, b, c \in \mathbb{Z}, \frac{b}{c}\) tối giản) là quảng đường vật di chuyển trong khoảng thời gian từ thời điểm t=0(s) đến thời điểm \(t=\frac{3 \pi}{4} . \text { Tính } P=2 a-3 b+2 c .\)

Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {\mathop{\rm s}\nolimits} {\rm{inx}} + 1\), trục hoành và hai đường thẳng \(x=0\) và \(x = {{7\pi } \over 6}\)