Tìm tất cả các giá trị thực của tham số m để hàm số có 3 điểm cực trị
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo saiĐể hàm số có ba cực trị thì trước hết hàm số phải là hàm số trùng phương tức m ≠ 0
Ta có:
Hàm số có 3 cực trị khi và chỉ khi y′ có 3 nghiệm phân biệt
Vậy các giá trị cần tìm của m là
ADMICRO
YOMEDIA
ZUNIA9
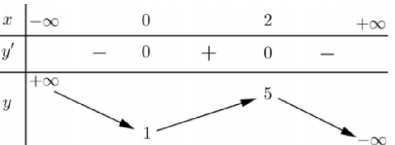
.jpg.png)
.png)