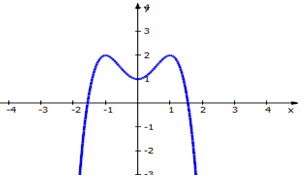
Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số \(y = {x^4} + 2m{x^2} + 1\) có ba điểm cực trị tạo thành một tam giác vuông cân.
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiHàm số \(y = {x^4} + 2m{x^2} + 1\) có tập xác định:
Ta có: \(y’ = 4{x^3} + 4mx\,;\,y’ = 0 \Leftrightarrow 4{x^3} + 4mx = 0 \Leftrightarrow 4x\left( {{x^2} + m} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} = – m\,\,\left( * \right)\end{array} \right.\)
Hàm số có 3 cực trị khi và chỉ khi phương trình \(\left( * \right)\) có 2 nghiệm phân biệt khác 0 \( \Leftrightarrow – m > 0 \Leftrightarrow m < 0\).
Vậy tọa độ 3 điểm lần lượt là: \(A\left( {0;1} \right)\,;\,B\left( { – \sqrt { – m} ;1 – {m^2}} \right)\,;\,C\left( {\sqrt { – m} ;1 – {m^2}} \right)\)
Ta có \(\overrightarrow {AB} = \left( { – \sqrt { – m} ; – {m^2}} \right)\,;\,\overrightarrow {AC} = \left( {\sqrt { – m} ; – {m^2}} \right)\)
Vì \(\Delta ABC\) vuông cân tại \(A \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = 0 \Leftrightarrow – \sqrt {{m^2}} + {m^2}.{m^2} = 0 \Leftrightarrow – \left| m \right| + {m^4} = 0 \Leftrightarrow m + {m^4} = 0\)
\( \Leftrightarrow m = – 1\) ( vì m < 0)
Vậy với m = – 1 thì hàm số có 3 cực trị tạo thành một tam giác vuông cân
Câu hỏi liên quan
-
Tìm tất các giá trị thực của tham số m để hàm số \(y=\frac{1}{3} x^{3}+(m+3) x^{2}+4(m+3) x+m^{3}-m\) đạt cực trị tại \(x_{1}, x_{2}\) thỏa mãn \(-1<x_{1}<x_{2}\)
-
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
.png)
Giá trị cực tiểu của hàm số đã cho bằng
-
Đồ thị hàm số \(y = {x^4} - 3{x^2} + 5\) có bao nhiêu điểm cực tiểu?
-
Hàm số \(y = \frac{{2x – 5}}{{x + 1}}\) có bao nhiêu điểm cực trị?
-
Cho hàm số y = f(x) có đồ thị là đường cong trong hình vẽ bên. Hàm số f(x) đạt cực tiểu tại điểm nào dưới đây?
-
Với giá trị nào của m, hàm số \(y = {x^3} - 2{x^2} + mx - 1\) không có cực trị?
-
Cho hàm số \(y = {x^3} - 2{x^2} + 3.\). Điểm M(0; 3) là:
-
Tìm các giá trị thực của tham số m để hàm số \(y = x³ - 3x² + m x + 1\) đạt cực đại tại x = 2
-
Số cực trị của hàm số \(f\left( x \right) = {{\rm{x}}^4} + 3{{\rm{x}}^2} - 5\) là
-
Cho hàm số y = f(x) có bảng biến thiên như hình bên. Mệnh đề nào dưới đây đúng?
.png)
-
Một ngọn hải đăng đặt tại vị trí A có khoảng cách đến bờ biển AB=5km. Trên bờ biển có một cái kho ở vị trí C cách B một khoảng 7km. Người canh hải đăng có thể chèo đò từ A đến M trên bờ biển với vận tốc 4km/h rồi đi bộ đến C với vận tốc 6km/h. Vị trí của điểm M cách B một khoảng bao nhiêu để người đó đi đến kho nhanh nhất?
-
Cho hàm số y=f(x) có \(f'\left( x \right) = \frac{1}{2}{x^3}{\left( {x - 1} \right)^2}\left( {2x - 1} \right){\left( {x + 2} \right)^5}\). Điểm cực tiểu của hàm số là
-
Tìm tất cả các giá trị của tham số m để hàm số \(y=\frac{1}{3} x^{3}-m x^{2}+(2 m-1) x-3\) có cực trị.
-
Hàm số y = x3 – 3x2 – 1 đạt cực đại tại?
-
Cho hàm số y=f(x) có bảng biến thiên như sau:
Giá trị cực đại của hàm số đã cho là:
-
Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = x3-3mx2+2 có hai điểm cực trị A: B sao cho A: B và M( 1; -2) thẳng hàng.
-
Hàm số y = x4 – 4x2 + 4 đạt cực tiểu tại những điểm nào?
-
Hàm số \(y = mx⁴ + (m -1) x² +1- 2m\)có một điểm cực trị khi
-
Cho hàm số \(y = f\left( x \right)\) xác định liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
.png)
Giá trị cực đại của hàm số là
-
Cho hàm số \(y=x^{3}+17 x^{2}-24 x+8\) . Kết luận nào sau đây là đúng?
