Trong các hình trụ nội tiếp hình cầu bán kính R, hình trụ có thể tích lớn nhất bằng
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiGọi chiều cao, bán kính đáy và thể tích của hình trụ nội tiếp hình cầu lần lượt là h, r và V. Khi đó
\(V=\pi r^{2} h . \text { Vì } r^{2}=R^{2}-\frac{h^{2}}{4} \text { nên } V=\pi\left(R^{2}-\frac{h^{2}}{4}\right) h=\pi\left(R^{2} h-\frac{h^{3}}{4}\right)\)
\(V(h)=\pi\left(R^{2} h-\frac{h^{3}}{4}\right), h \in(0 ; 2 R) ; V^{\prime}(h)=\pi\left(R^{2}-\frac{3 h^{2}}{4}\right) ; V^{\prime}(h)=0 \Leftrightarrow h=\frac{2 R}{\sqrt{3}}\)
Bảng biến thiên
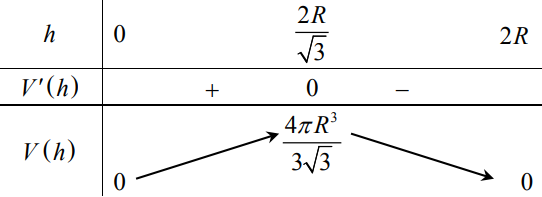
Vậy hình trụ nội tiếp hình cầu bán kính R có thể tích lớn nhất khi chiều cao của nó bằng \(\frac{2 R}{\sqrt{3}}\) .
Khi đó, thể tích hình trụ là \(\frac{4 \pi R^{3}}{3 \sqrt{3}}\).
.jpg.png)
.jpg.png)