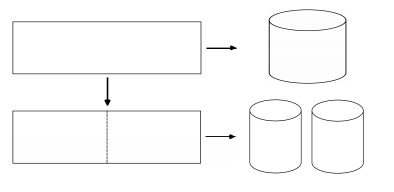
Từ một tấm tôn hình chữ nhật kích thước 50cm x 240cm, người ta làm các thùng đựng nước hình trụ có chiều cao bằng 50cm, theo hai cách sau (xem hình minh họa dưới đây): - Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng. - Cách 2: Cắt tấm tôn ban đầu thành hai tấm bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng. Kí hiệu (V1) là thể tích của thùng gò được theo cách 1 và (V2) là tổng thể tích của hai thùng gò được theo cách 2. Tính tỉ số \( \frac{{{V_1}}}{{{V_2}}}\)
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiCách 1: Chu vi đáy là
\(\begin{array}{l} 240cm \Rightarrow 2\pi {R_1} = 240 \Leftrightarrow {R_1} = \frac{{120}}{\pi }\\ \Rightarrow {V_1} = \pi R_1^2h = \pi {\left( {\frac{{120}}{\pi }} \right)^2}h = \frac{{{{120}^2}.50}}{\pi } \end{array}\)
Cách 2: Chu vi đáy mỗi hình trụ nhỏ là:
\(\begin{array}{l} 240cm \Rightarrow 2\pi {R_1} = 240 \Leftrightarrow {R_1} = \frac{{120}}{\pi }\\ \Rightarrow {V_1} = \pi R_1^2h = \pi {\left( {\frac{{120}}{\pi }} \right)^2}h = \frac{{{{120}^2}.50}}{\pi } \end{array}\)
Vậy \( \frac{{{V_1}}}{{{V_2}}} = \frac{{{{120}^2}.50}}{\pi }:\frac{{{{2.60}^2}.50}}{\pi } = 2\)
Một đường tròn có bán kính r thì có chu vi và diện tích lần lượt là
\( C = 2\pi r;S = \pi {r^2} \Rightarrow S = \frac{{{C^2}}}{{4\pi }}\)
Gọi chiều dài tấm tôn là a thì tổng diện tích đáy của thùng theo 2 cách lần lượt là \( {S_1} = \frac{{{a^2}}}{{4\pi }};{S_2} = 2.\frac{{{{\left( {\frac{a}{2}} \right)}^2}}}{{4\pi }} = \frac{{{a^2}}}{{8\pi }} \Rightarrow \frac{{{S_1}}}{{{S_2}}} = 2 \Rightarrow \frac{{{V_1}}}{{{V_2}}} = 2\)
Câu hỏi liên quan
-
Cắt một khối trụ bởi một mặt phẳng ta được một khối \(\left( H \right)\) như hình vẽ. biết rằng thiết diện là một elip có độ dài trục lớn là \(10\), khoảng cách từ điểm thuộc thiết diện gần mặt đáy nhất và điểm thuộc thiết diện xa mặt đáy nhất tới mặt đáy lần lượt là 8 và \(14\). Tính thể tích của \(\left( H \right)\)
.PNG)
-
Hình trụ (T) được sinh ra khi quay hình chữ nhật ABCD quanh cạnh AB. Biết \(AC = a\sqrt2,\,\,\widehat {ABC} = 45^0\) . Diện tích toàn phần Stp của hình trụ (T) là
-
Cho hình cầu tâm O, đường kính 2R và hình trụ tròn xoay nội tiếp trong hình cầu. Hãy tìm kích thước của hình trụ khi nó có thể tích đạt giá trị lớn nhất.
-
Cho hình vuông ABCD có cạnh bằng a. Gọi M,N lần lượt là trung điểm của AB và CD. Khi quay hình vuông ABCD quanh MN tạo thành một hình trụ. Gọi ( S ) là mặt cầu có diện tích bằng diện tích toàn phần của hình trụ, ta có bán kính của mặt cầu ( S ) là:
-
Một nóc tòa nhà cao tầng có dạng hình nón. Người ta muốn xây một bể nước có dạng một hình trụ nội tiếp trong hình nón để chứa nước (như hình vẽ minh họa). Cho biết SO = h;OB = R;OH = x (0 < x < h). Tìm thể tích lớn nhất của hình trụ.
.png)
-
Thể tích V của khối trụ có chiều cao bằng a và đường kính đáy bằng \(a\sqrt2\) là?
-
Cho hình nón có bán kính đáy là \(r = \sqrt 2 \) và độ dài đường sinh \(l = 4\). Tính diện tích xung quanh S của hình nón đã cho.
-
Một khối trụ có thể tích bằng \(16\pi .\) Nếu chiều cao khối trụ tăng lên hai lần và giữ nguyên bán kính đáy thì được khối trụ mới có diện tích xung quanh bằng \(16\pi .\) Bán kính đáy của khối trụ ban đầu là
-
Cho khối nón có độ dài đường cao bằng (2a ) và bán kính đáy bằng (a. ) Thể tích của khối nón đã cho bằng:
-
Cho hình chữ nhật (ABCD ), khi quay hình chữ nhật quanh cạnh (AD ) thì (CD ) được gọi là:
-
Mệnh đề nào dưới đây đúng? Cho hình chữ nhật ABCD có AB = 2AD. Quay hình chữ nhật đã cho quanh AD và AB ta được hai hình trụ tròn xoay có thể tích lần lượt là V1, V2.
-
Cắt hình nón bởi một mặt phẳng qua trục thu được thiết diện là một tam giác vuông có diện tích bằng 8. Diện tích xung quanh của hình nón đã cho bằng:
-
Cho hình nón có bán kính đường tròn đáy bằng R, chiều cao bằng h, độ dài đường sinh bằng \(l\). Khẳng định nào sau đây là đúng?
-
Cho một hình trụ có bán kính đáy R, chiều cao h và thể tích V1; một hình nón có đáy trùng với một đáy của hình trụ, có đỉnh trùng với tâm đáy còn lại của hình trụ (hình vẽ bên dưới) và có thể tích V2.
Khẳng định nào sau đây là khẳng định đúng ?
.png)
-
Cho hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh huyền 2a. Thể tích của khối nón bằng
-
Thể tích khối trụ có bán kính (r = 4cm ) và chiều cao (h = 5cm ) là:
-
Cho hình nón có bán kính đáy là 4a, chiều cao là 3a. Diện tích toàn phần hình nón là
-
Cho hình chữ nhật ABCD có AB = 2AD. Lần lượt quay hình chữ nhật quanh các trục AB, AD ta được hai khối trụ lần lượt gọi là (H1), (H2). Tính tỉ số thể tích của khối trụ (H1) chia cho thể tích của khối trụ (H2)
-
Một cái phễu rỗng phần trên có kích thước như hình vẽ. Diện tích xung quanh của phễu là:
-
Bán kính đáy của khối trụ tròn xoay có thể tích bằng V và chiều cao bằng h là:
