Với m > 0 phương trình \(\left| x \right| = \sqrt[3]{{2{x^2} - \left| x \right| + m - 1}}\) có ít nhất mấy nghiệm?
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo sai\(\left| x \right| = \sqrt[3]{{2{x^2} - \left| x \right| + m - 1}} \Leftrightarrow {\left| x \right|^3} - 2{x^2} + \left| x \right| + 1 = m\)
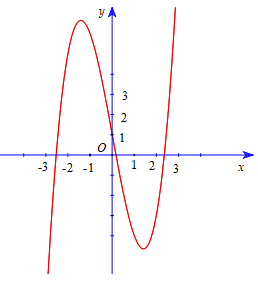
Đồ thị hàm số \(y = |x{|^3} - 2{x^2} + \left| x \right| + 1\) có dạng như hình (2)
Số nghiệm của phương trình \(|x{|^3} - 2{x^2} + \left| x \right| + 1 = m\) là số giao điểm của đồ thị hàm số và đường thẳng y = m.
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số và đường thẳng y = m.
Dựa vào đồ thị với m > 0 phương trình có tối thiểu 0 nghiệm ( 0 nghiệm – tức là phương trình vô nghiệm).
ADMICRO
YOMEDIA
ZUNIA9
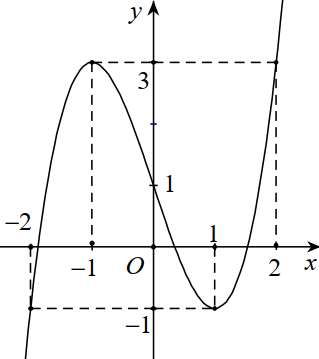
.png)
.png)