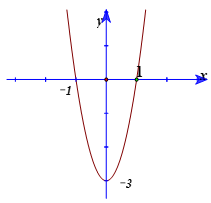
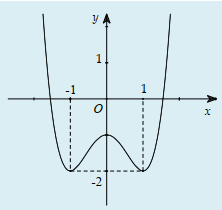
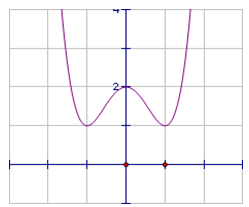
Cho hàm số y = f(x) = ax³+ bx²+ cx+ d có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y = 4 tại điểm có hoành độ âm và đồ thị hàm số y = f’(x) cho bởi hình vẽ bên. Tìm hàm số đã cho ?

Câu hỏi liên quan

• Tìm tập hợp tất cả các giá trị của tham số m sao cho bất phương trình sau có nghiệm:\(\sqrt{x+5}+\sqrt{4-x} \geq m\)

• Cho hàm số y=f(x) xác định, liên tục trên \(\mathbb{R}\) và có đồ thị như hình bên. Đồ thị nào dưới đây là đồ thị của hàm số y=f(x)+1?

  

• Đường cong trong hình vẽ dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

  

ZUNIA12

• Tìm số giao điểm của đồ thị (C): y = x³ + x – 2 và đường thẳng y = x – 1

• Cho hàm số \(y = \frac{{2x + 1}}{{x + 1}}\) có đồ thị (C) và đường thẳng d: y = x + m. Giá trị của tham số m để d cắt (C) tại hai điểm phân biệt A, B sao cho \(AB = \sqrt {10} \) là

• Cho hàm số y = 2x³ - 3x² + 1  có đồ thị và đường thẳng  d: y = x - 1. Giao điểm của (C) và d  lần lượt là A(1; 0); B và C. Khi đó khoảng cách giữa B và C là

• Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

  

   

• Cho hàm số \(y=x^{4}-4 x^{2}-2\) có đồ thị (C) và đường thẳng \(d: y=m\) . Tất cả các giá trị của tham số m để d cắt (C) tại bốn điểm phân biệt là
   

• Cho hàm số y = x³ + ax² + bx + c đi qua điểm A(0;-4) và đạt cực đại tại điểm B(1;0) hệ số góc k của tiếp tuyến với đồ thị hàm số tại điểm có hoành độ bằng -1 là:

• Đồ thị (C) của hàm số \(y = \frac{{2x - 8}}{x}\) cắt đường thẳng Δ: y = - x tại hai điểm phân biệt A và B. Tìm tọa độ trung điểm I của đoạn thẳng AB

• Với m > 0 phương trình \(\left| x \right| = \sqrt[3]{{2{x^2} - \left| x \right| + m - 1}}\) có ít nhất mấy nghiệm? 

• Cho hàm số: \(y = {x^3} + 2m{x^2} + 3(m – 1)x + 2\) có đồ thị (C). Đường thẳng d:y = – x + 2 cắt đồ thị (C) tại ba điểm phân biệt \(A\left( {0; – 2} \right),{\rm{ }}B\) và C. Với M(3;1), giá trị của tham số m để tam giác MBC có diện tích bằng \(2\sqrt 7 \) là

• Đồ thị hàm số \(y = \cos x\) cắt trục tung tại điểm có tung độ bằng

• Cho hàm số y=f(x) có bảng biến thiên sau

  

  Số nghiệm của phương trình \(2 f(x)+3=0\) là?

• Đường thẳng\((C): y=\frac{2 x-1}{x+1}\) cắt đồ thị hàm số \(d: y=2 x-3\) tại các điểm có tọa độ là

   

• Biết đồ thị hàm số \( y = \frac{{2x - 1}}{{x + 3}}\) cắt trục Ox,Oy lần lượt tại hai điểm phân biệt A, B.  Tính diện tích S của tam giác OAB

• Đồ thị sau đây là đồ thị  của hàm số nào?

  

   

• Cho hàm số y = x⁴ − 2mx² − m.  Với giá trị nào của mm thì đồ thị hàm số có ba điểm cực trị đồng thời ba điểm cực trị đó tạo thành một tam giác vuông cân.

• Đồ thị sau đây là của hàm số nào?

  

• Phương trình tiếp tuyến của đồ thị hàm số \(y = {x^4} - 2{x^2} - 3\) song song với đường thẳng y = 24x - 1 là: