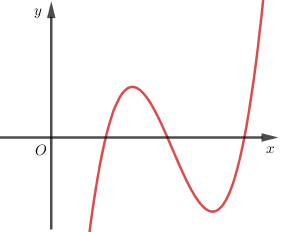
Cho hàm số y = 2x³- 3x²+ 1 có đồ thị và đường thẳng d: y = x - 1. Giao điểm của (C) và d lần lượt là A(1; 0); B và C. Khi đó khoảng cách giữa B và C là

A. \(BC= \frac{{\sqrt {30} }}{2}\)

B. \(BC= \frac{{\sqrt {34} }}{2}\)

C. \(BC = \frac{{3\sqrt 2 }}{2}\)

D. \(BC= \frac{{\sqrt {14} }}{2}\)

Sai B là đáp án đúng Xem lời giải

Chính xác Xem lời giải

Suy nghĩ và trả lời câu hỏi trước khi xem đáp án

ATNETWORK

Môn: Toán Lớp 12

Chủ đề: Ứng Dụng Đạo Hàm Để Khảo Sát Và Vẽ Đồ Thị Của Hàm Số

Bài: Khảo sát sự biến thiên và vẽ đồ thị của hàm số

Lời giải:

Báo sai

\(\begin{array}{l}
2{x^3} - 3{x^2} + 1 = x - 1\\
\Leftrightarrow 2{x^3} - 3{x^2} - x + 2 = 0\\
\Leftrightarrow \left( {x - 1} \right)\left( {2{x^2} - x - 2} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x = 1\\
2{x^2} - x - 2 = 0\,\,\left( 1 \right)
\end{array} \right.
\end{array}\)

Khi đó ta có A(1 ; 0) ; B( x₁ ; x₁-1) và C( x₂ ; x₂-1) (x₁ ; x₂ là nghiệm của (1))

Ta có \(\overrightarrow {BC} = \left( {{x_2} - {x_1};{x_2} - {x_1}} \right)\), suy ra

\(\begin{array}{*{20}{l}}
{BC = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{x_2} - {x_1}} \right)}^2}} = \sqrt {2{{\left( {{x_2} - {x_1}} \right)}^2}} }\\
{ = \sqrt {2{{\left( {{x_2} + {x_1}} \right)}^2} - 4{x_1}{x_2}} = \sqrt {2\left( {\frac{1}{4} + 4} \right)} = \frac{{\sqrt {34} }}{2}}
\end{array}\)

ADMICRO

YOMEDIA

Câu hỏi liên quan

Qua điểm A( 0;2 ) có thể kẻ được bao nhiêu tiếp tuyến với đồ thị của hàm số y = x⁴-2x²+2?
Với giá trị nào của mmthì đường thẳng y = −x + m cắt đồ thị hàm số \(\left( C \right):y = \frac{{x - 2}}{{1 - x}}\) tại hai điểm phân biệt là
Đường cong hình bên là đồ thị của một hàm số nào trong bốn hàm số dưới đâ?

ZUNIA12

Tìm m để đồ thị hàm số y = x³+mx+² cắt trục hoành tại một điểm duy nhất.
Cho các phát biểu sau:

I. Đồ thị hàm số có y = x⁴ – x + 2 có trục đối xứng là Oy.

II. Hàm số f(x) liên tục và có đạo hàm trên khoảng (a;b) đạt cực trị tại điểm x0 thuộc khoảng (a;b) thì tiếp tuyến tại điểm M(x⁰,f(x₀)) song song với trục hoành.

III. Nếu f(x) nghịch biến trên khoảng (a;b) thì hàm số không có cực trị trên khoảng (a;b).

IV. Hàm số f(x) xác định và liên tục trên khoảng (a;b) và đạt cực tiểu tại điểm x0 thuộc khoảng (a;b) thì f(x) nghịch biến trên khoảng (a;x₀) và đồng biến trên khoảng (x₀;b).

Các phát biểu đúng là:
Tìm tất cả các giá trị thực của tham số m sao cho phương trình \(\sqrt{x^{2}-4 x+5}=m+4 x-x^{2}\) có đúng 2 nghiệm dương?
Cho hàm số y = x³-3x²+4 có đồ thị (C). Gọi d là đường thẳng qua I(1; 2) với hệ số góc k . Có bao nhiêu giá trị nguyên của k để d cắt (C) tại ba điểm phân biệt I, A, B sao cho I là trung điểm của đoạn thẳng AB là
Tìm m để phương trình \({x^4} - 2{x^2} + 3--{m^2} + 2m = 0\) có đúng ba nghiệm phân biệt
Xác định giá trị của tham số \(m\) để hàm số \(y = {x^3} - 3\left( {m - 1} \right){x^2} - 3\left( {m + 1} \right)x - 5\) có cực trị.
Cho hàm số y = x³-3x²-m-1 có đồ thị (C). Giá trị của tham số m để đồ thị (C) cắt trục hoành tại ba điểm phân biệt lập thành cấp số cộng là
Có bao nhiêu điểm thuộc đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9iabgkHiTiaadIhadaahaaWcbeqaaiaaiodaaaGccqGHsislcaaI % ZaGaamiEaiabgUcaRiaaiodaaaa!3F1C! y = - {x^3} - 3x + 3\) cách giao điểm của đồ thị hàm số với trục tung một khoảng bằng \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaOaaaeaaca % aIXaGaaG4naaWcbeaaaaa!378B! \sqrt {17} \)?
Một cái hộp có dạng hình hộp chữ nhật có thể tích bằng 48 và chiều dài gấp đôi chiều rộng. Chất liệu làm đáy và 4 mặt bên của hộp có giá thành gấp ba lần giá thành của chất liệu làm nắp hộp. Gọi hh là chiều cao của hộp để giá thành của hộp là thấp nhất. Biết \( h = \frac{m}{n}\)với m, n là các số nguyên dương nguyên tố cùng nhau. Tổng m+n là
Biết \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqamaabm % aabaGaamiEamaaBaaaleaacaWGbbaabeaakiaacUdacaaMc8UaamyE % amaaBaaaleaacaWGbbaabeaaaOGaayjkaiaawMcaaaaa!3E80! A\left( {{x_A};\,{y_A}} \right)\),\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOqamaabm % aabaGaamiEamaaBaaaleaacaWGcbaabeaakiaacUdacaaMc8UaamyE % amaaBaaaleaacaWGcbaabeaaaOGaayjkaiaawMcaaaaa!3E83! B\left( {{x_B};\,{y_B}} \right)\) là hai điểm thuộc hai nhánh khác nhau của đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOqamaabm % aabaGaamiEamaaBaaaleaacaWGcbaabeaakiaacUdacaaMc8UaamyE % amaaBaaaleaacaWGcbaabeaaaOGaayjkaiaawMcaaaaa!3E83! B\left( {{x_B};\,{y_B}} \right)\) sao cho đoạn thẳng AB có độ dài nhỏ nhất. Tính \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuaiabg2 % da9iaadIhadaqhaaWcbaGaamyqaaqaaiaaikdaaaGccqGHRaWkcaWG % 4bWaa0baaSqaaiaadkeaaeaacaaIYaaaaOGaey4kaSIaamyEamaaBa % aaleaacaWGbbaabeaakiaac6cacaWG5bWaaSbaaSqaaiaadkeaaeqa % aaaa!439D! P = x_A^2 + x_B^2 + {y_A}.{y_B}\).
Cho hàm số f(x) = x³-3x2+ 2 có đồ thị là đường cong trong hình bên. Tìm tất cả các giá trị thực của tham số m đề phương trình |x|³−3x²+2 = mx3-3x²+2 = m có nhiều nghiệm thực nhất
Đường cong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hàm số đó là hàm số nào?
Tất cả giá trị của tham số m để phương trình \({x^4} – 2{x^2} – m + 3 = 0\) có hai nghiệm phân biệt là
Đường cong trong hình bên dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
Đồ thị sau đây là của hàm số nào?
Ðường cong trong hình dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
Cho hàm số \(y=\frac{2x-1}{x-1}\)có đồ thị như hình bên. Đồ thị nào dưới đây là đồ thị của hàm số \(y=\frac{|2x-1|}{x-1}\)