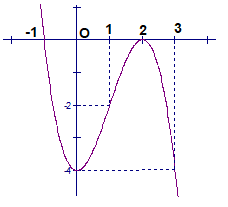
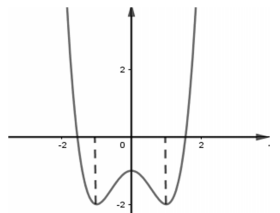
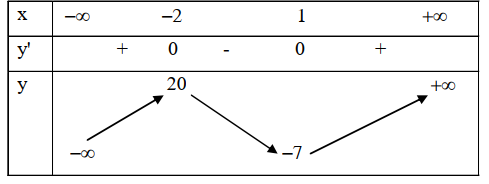
Cho hàm số y=f(x) liên tục trên đoạn [-2;2] và có đồ thị là đường cong như trong hình vẽ bên.

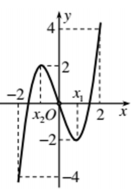
Hỏi phương trình \(|f(x)-1|=2\) có mấy nghiệm phân biệt trên [-2;2]?

Câu hỏi liên quan

• Tìm m  để đồ thị hàm số  y = x³+mx+² cắt trục hoành tại một điểm duy nhất.

• Trong các đồ thị hàm số sau, đồ thị nào là đồ thị của hàm số \(y\; = \;\frac{x}{{\left| {x\; - \;1} \right|}}\) ?

• Đồ thị hàm số \(y = \frac{{3{x^2} - 4x + 1}}{{x - 1}}\)

ZUNIA12

• Bảng biến thiên sau là của hàm số nào?

  

   

• Tiệm cận ngang của đồ thị hàm số \((H): y=\frac{x+2}{x+1}\) cắt đồ thị hàm số \((C): y=2 x^{4}-x^{2}\) tại các điểm có tọa độ là
   

• Tìm tất cả các giá trị thực của tham số m sao cho phương trình \(3 \sqrt{x-1}+m \sqrt{x+1}=2 \sqrt[4]{x^{2}-1}\) có hai nghiệm thực?

• Cho hàm số \(y = \frac{{mx - 1}}{{x + 2}}\) có đồ thị là (C) . Tìm m để đường thẳng d: y = 2x-1 cắt đồ thị (C) tại hai điểm phân biệt A; B  sao cho AB = \(\sqrt {10} \)

• Đồ thị hàm số \(y = {\log _2}\left( {{x^2} + 2} \right)\) cắt trục tung tại điểm có tung độ bằng

• Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình: \(-x^{3}+3 m x-2<-\frac{1}{x^{3}}\) nghiệm đúng \(\forall x \geq 1 ?\)

• Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

• Đồ thị hàm số \(y = {e^{2x}}\) cắt trục tung tại điểm có tung độ bằng

• Cho hàm số y = 2x³ - 3x² + 1  có đồ thị và đường thẳng  d: y = x - 1. Giao điểm của (C) và d  lần lượt là A(1; 0); B và C. Khi đó khoảng cách giữa B và C là

• Cho hàm số \(y = \frac{{2x – 1}}{{x + 1}}\) có đồ thị (C) và đường thẳng d: y = 2x – 3. Đường thằng d cắt (C) tại hai điểm A và B. Khoảng cách giữa A và B là

• Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
  

  Phương trình f(x)-2=0 có tất cả bao nhiêu nghiệm?

• Với giá trị nào của mmthì đường thẳng y = −x + m cắt đồ thị hàm số \(\left( C \right):y = \frac{{x - 2}}{{1 - x}}\) tại hai điểm phân biệt là

• Số giao điểm của đồ thị hàm số \(y=\frac{x^{2}-4 x+3}{x+2}\)và trục hoành là

• Cho hàm số \(y = \frac{{x + 2}}{{2x + 3}}\left( 1 \right)\). Viết phương trình tiếp tuyến của đồ thị hàm số đã cho, biết tiếp tuyến đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A; B và tam giác OAB cân tại gốc tọa độ.

• Cho hàm số y = f(x) có đạo hàm trên (a;b) . Phát biểu nào sau đây là đúng ?

• Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình \(\sqrt{(1+2 x)(3-x)}>m+2 x^{2}-5 x-3\) nghiệm đúng với mọi \(x \in\left[-\frac{1}{2} ; 3\right] ?\)

• Đồ thị sau đây là của hàm số nào: