Trắc nghiệm Hệ tọa độ trong không gian Toán Lớp 12
-
Câu 1:
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):x+y−2z−1=0 và đường thẳng \(d:\frac{{x - 2}}{1} = \frac{{y - 2}}{1} = \frac{z}{{ - 2}}\). Tọa độ giao điểm của d và (P) là
-
Câu 2:
Số phức z = a + bi được biểu diễn trên mặt phẳng phức là tiếp điểm của một tiếp tuyến đi qua gốc tọa độ O(0;0) với đường tròn (C):(x−3)2 + (y−4)2 = 4 trên mặt phẳng phức đó. Khoảng cách từ O đến tiếp điểm bằng
-
Câu 3:
Trong không gian với hệ tọa độ Oxyz, cho sáu điểm A(0;1;2), B(2;−1;−2); C(3;1;2), A′, B′, C′ thỏa mãn
-
Câu 4:
Trong không gian với hệ tọa độ Oxyz, cho điểm I(1;2;−1) và mặt phẳng (α) có phương trình 2x−2y−z+4 = 0. Mặt cầu (S) có tâm II tiếp xúc với (α) tại H. Tọa độ điểm H là
-
Câu 5:
Trong không gian với hệ tọa độ Oxyz, cho các điểm A(1;2;2),B(2;1;3),C(3;0;4). Khẳng định nào sau đây là đúng?
-
Câu 6:
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(−3;4;2), B(−5;6;2), C(−4;7;−1). Tìm tọa độ điểm D thỏa mãn \(\overrightarrow {AD} = 2\overrightarrow {AB} + 3\overrightarrow {AC} .\)
-
Câu 7:
Trong không gian với hệ tọa độ Oxyz , cho hai điểm M(1;2;3) và N(2;1;−2). Phương trình mặt phẳng (P) chứa hai điểm M,N và song song với trục Ox là
-
Câu 8:
Nếu phép tịnh tiến biến điểm A(1;2) thành điểm A′(−2;3) thì nó biến điểm B(0;1) thành điểm nào?
-
Câu 9:
Trong không gian hệ tọa độ Oxyz, đường thẳng dd đi qua điểm A(1;1;1) và có một véctơ chỉ phương là \(\vec u\left( {1;0; - 1} \right)\) có phương trình là
-
Câu 10:
Với giá trị nào của mm thì điểm A(1;2) và hai điểm cực trị của đồ thị hàm số y = x3 + 3x2 + m thẳng hàng?
-
Câu 11:
Cho hàm số \(y = \frac{{2x}}{{x + 1}}\). Tìm điểm M thuộc đồ thị (C), biết tiếp tuyến của (C) tại M cắt Ox và Oy tại hai điểm A,B và ΔOAB có diện tích bằng \(\frac{1}{4}\)
-
Câu 12:
Cho M(2;−5;7). Tìm tọa độ điểm đối xứng của M qua mặt phẳng Oxy
-
Câu 13:
Cho hai đường thẳng d:x+y−1=0 và d′:x+y−5=0. Phép tịnh tiến theo vecto \(\vec u\) biến đường thẳng d thành d’. Khi đó, độ dài bé nhất của \(\vec u\) là bao nhiêu?
-
Câu 14:
Cho z = 1 + 2i, số phức z′ đối xứng với số phức z qua gốc tọa độ O(0;0) là
-
Câu 15:
Cho tam giác ABC có A(2;3),B(1;−2),C(6;2). Phép tịnh tiến \({T_{\overrightarrow {BC} }}\) biến tam giác ABC thành tam giác A′B′C′. Tọa độ trọng tâm tam giác A′B′C′ là
-
Câu 16:
Cho i là đơn vị ảo. Cho m ∈ R. Trên mặt phẳng tọa độ Oxy, điểm biểu diễn hình học số phức z = mi có tọa độ là
-
Câu 17:
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình lần lượt
\(d:{\mkern 1mu} x = 1 + 2t,{\mkern 1mu} y = 2 - t,{\mkern 1mu} z = 3t.\). Tìm tọa độ điểm K đối xứng với điểm I(2;−1;3) qua đường thẳng d. -
Câu 18:
Tích có hướng của hai véctơ \(\vec{u}(-2 ; 1 ; 0), \vec{v}(0 ; 3 ; 2)\) là
-
Câu 19:
Tích có hướng của hai véctơ \(\vec{u}(-3 ; 5 ;-1), \vec{v}(4 ;-3 ;-2)\) là:
-
Câu 20:
Tích có hướng của hai véc tơ \(\vec{u}(1 ; 3 ; 0), \vec{v}(3 ; 2 ; 1) \) là
-
Câu 21:
Tích có hướng của hai véctơ \(\vec{u}(2 ; 5 ; 5), \vec{v}(4 ; 0 ; 0) \) là:
-
Câu 22:
Tích có hướng của hai véctơ \(\vec{u}(9,4 ; 0), \vec{v}(-1 ; 2 ;-3) \) là:
-
Câu 23:
Tích có hướng của hai véctơ \(\vec{u}(1 ; 1 ; 4), \vec{v}(2 ; 0 ; 5) \) là:
-
Câu 24:
Tích có hướng của hai véctơ \(\vec{u} (4 ; 2 ; 1), \vec{v}(1 ; 1 ; 3)\) là:
-
Câu 25:
Tích có hướng của hai véctơ \(\vec{u}(0 ; 2 ; 0), \vec{v}(3 ; 1 ; 0) \) là:
-
Câu 26:
Tích có hướng của hai véctơ \(\vec{u}(2 ; 1 ; 1), \vec{v}(4 ; 3 ; 1) \) là:
-
Câu 27:
Tích có hướng của hai véctơ \(\vec{u}(1 ; 2 ; 3), \vec{v}(0 ;-2 ;-5) \) là:
-
Câu 28:
Tích vô hướng của hai vecto \(\vec{u} (3 ; 2 ; 0), \vec{v}(1 ; 3 ; 4) \) là
-
Câu 29:
Tích có hướng của hai vecto \(\vec{u} (1 ; 3 ;-5), \vec{v}(0 ; 1:-2) \) là:
-
Câu 30:
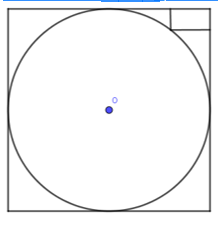
Cho hình trụ (T) có (C),(C′) là hai đường tròn đáy nội tiếp hai mặt đối diện của một hình lập phương. Biết rằng, trong tam giác cong tạo bởi đường tròn (C) và hình vuông ngoại tiếp của (C) có một hình chữ nhật kích thước 1×2 (như hình vẽ dưới đây). Thể tích của khối trụ (T) là
-
Câu 31:
Một trang chữ của một quyển sách tham khảo Văn học có diện tích 384 cm2. Trang chữ này được trình bày trên một trang giấy được canh lề trái là 2cm, lề phải là 2 cm, lề trên 3 cm và lề dưới là 3 cm. Hỏi trang giấy nhỏ nhất cần dùng có chiều dài và chiều rộng là:
-
Câu 32:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a,a,đường cao SA=x. Góc giữa (SBC) và mặt đáy bằng 600. Khi đó x bằng
-
Câu 33:
Trong không gian với hệ tọa độ Oxyz cho 4 điểm A(0 ; 0 ; 3), B(1 ; 1 ; 5), C(-3 ; 0 ; 0), D(0 ;-3 ; 0) Chứng minh 4 điểm A, B, C, D đồng phằng và tính diện tích \(\triangle A C D\)
-
Câu 34:
\(\text { Trong không gian với hệ tọa độ } O x y z \text { cho } 3 \text { điểm } A(2 ; 3 ;-1), B(-1 ; 0 ; 2), C(1 ;-2 ; 0)\).
Cho F là phân giác trong của tam giác ABC. Xác định tọa độ điểm F.
-
Câu 35:
\(\text { Trong không gian với hệ tọa độ } O x y z \text { cho } 3 \text { điểm } A(2 ; 3 ;-1), B(-1 ; 0 ; 2), C(1 ;-2 ; 0)\). \(\text { Tìm tọa độ điểm } H \text { trên } O x \text { sao cho } D H \perp A C\)
-
Câu 36:
\(\text { Trong không gian với hệ tọa độ } O x y z \text { cho } 3 \text { điểm } A(2 ; 3 ;-1), B(-1 ; 0 ; 2), C(1 ;-2 ; 0)\). \(\text { Tìm tọa độ điểm } E \text { trên }(O y z) \text { sao cho } A E / / B C\).
-
Câu 37:
\(\text { Trong không gian với hệ tọa độ } O x y z \text { cho } 3 \text { điểm } A(2 ; 3 ;-1), B(-1 ; 0 ; 2), C(1 ;-2 ; 0)\).
Tìm tọa độ điểm D trên Oz sao cho tứ diện ABCD có thể tích bằng 4
-
Câu 38:
\(\text { Trong không gian với hệ tọa độ } O x y z \text { cho } 3 \text { điểm } A(2 ; 3 ;-1), B(-1 ; 0 ; 2), C(1 ;-2 ; 0)\).
Tính diện tích tam giác ABC
-
Câu 39:
\(\text { Trong không gian } O x y z \text { cho } 4 \text { điểm } A(2 ;-1 ; 6), B(-3 ;-1 ;-4), C(5 ;-1 ; 0) \text { và } D(1 ; 2 ; 1) \text {. }\)
-
Câu 40:
\(\text { Cho ba điểm } A(2 ; 5 ; 3) ; B(3 ; 7 ; 4) ; C(x ; y ; 6) \text {. Tìm } x ; y \text { để } A, B, C \text { thẳng hàng? }\)
-
Câu 41:
\(\text { Cho vectơ } \vec{a}=(2 \sqrt{2} ;-1 ; 4) \text {. Tìm vectơ } \vec{b} \text { cùng phương với } \vec{a} \text { biết } \vec{a} \cdot \vec{b}=20 \text {. }\)
-
Câu 42:
\(\begin{aligned} \text { Cho hai vectơ } \vec{a}=(2 ; 3 ;-1) ; \vec{b}=(0 ;-2 ; 1) \text {. }\text { Tính } [\vec{a}+2 \vec{b} ; 5 \vec{a}-3 \vec{b}] \text {. } \end{aligned} \)
-
Câu 43:
\(\begin{aligned} \text { Cho hai vectơ } \vec{a}=(2 ; 3 ;-1) ; \vec{b}=(0 ;-2 ; 1) \text {. }\text { Tính }[\vec{a} ; \vec{b}] \text {. } \end{aligned} \)
-
Câu 44:
\(\begin{aligned} \text { Cho hai vectơ } \vec{a}=(2 ; 3 ;-1) ; \vec{b}=(0 ;-2 ; 1) \text {. }\text { Tính } \vec{a} \cdot \vec{b} \text {. } \end{aligned} \)
-
Câu 45:
\(\begin{aligned} &\text { Cho hai vectơ } \vec{a}=(2 ; 3 ;-1) ; \vec{b}=(0 ;-2 ; 1) \text {. }\\ &\text { Tính } \vec{b}+5 \vec{a} \text {. } \end{aligned} \)
-
Câu 46:
\(\begin{aligned} &\text { Cho hai vectơ } \vec{a}=(2 ; 3 ;-1) ; \vec{b}=(0 ;-2 ; 1) \text {. }\\ &\text { Tính } 2 \vec{a}+2 \vec{b}\text {. } \end{aligned} \)
-
Câu 47:
Trong không gian với hệ trục tọa độ Oxyz, cho hình hộp ABCD.EFGH với A(1 ; 1 ; 1), B(2 ; 1 ; 2),E(-1 ; 2 ;-2), D(3 ; 1 ; 2). Khoảng cách từ A đến mp(DCGH) bằng?
-
Câu 48:
\(\begin{aligned} &\text { Trong không gian với hệ trục tọa độ } O x y z \text {, cho } 4 \text { điểm } A(1 ; 0 ; 1), B(-1 ; 1 ; 2), C(-1 ; 1 ; 0\\ &D(2 ;-1 ;-2) \text {. Tính độ dài đường cao của tứ diện qua đỉnh A. } \end{aligned}\)
-
Câu 49:
\(\begin{aligned} &\text { Trong không gian với hệ trục tọa độ } O x y z, \text { cho } 4 \text { điểm } A(1 ; 0 ; 1), \quad B(-1 ; 1 ; 2), C(-1 ; 1 ; 0) \text {, }\\ &D(2 ;-1 ;-2) \text {. Tính thể tích tứ diện ABCD. } \end{aligned}\)
-
Câu 50:
\(\text { Trong không gian với hệ trục tọa độ } O x y z \text {, cho các điểm } A(1 ; 2 ; 3), B(2 ; 1 ; 1)\). \(\text { Tìm tọa độ điểm } M \in m p(O y z) \text { sao cho } 3 \text { điểm } A, B, M \text { thẳng hàng. }\)