Biết rằng tập hợp tất cả các giá trị của tham số m để phương trình sau \({{\rm{x}}^2} - x + 2\left( {1 - x} \right)\sqrt {x - m} - m = 0\) có 3 nghiệm phân biệt là \(\left[ {a;b} \right)\). Tính \(a + b\)?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có \({x^2} - x + 2\left( {1 - x} \right)\sqrt {x - m} - m = 0\)
\(\begin{array}{l} \Leftrightarrow {\left( {1 - x} \right)^2} + 2\left( {1 - x} \right)\sqrt {x - m} + \left( {x - m} \right) = 1\\ \Leftrightarrow {\left[ {1 - x + \sqrt {x - m} } \right]^2} = 1\\ \Leftrightarrow \left[ \begin{array}{l}1 - x + \sqrt {x - m} = 1\\1 - x + \sqrt {x - m} = - 1\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\sqrt {x - m} = x\\\sqrt {x - m} = x - 2\end{array} \right.\end{array}\)
\( \Rightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x - m = {x^2}\\x \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = x - {x^2}\\x \ge 0\end{array} \right.\\\left\{ \begin{array}{l}x - m = {x^2} - 4x + 4\\x \ge 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = - {x^2} + 5x - 4\\x \ge 2\end{array} \right.\end{array} \right.\)
Xét \(y = x - {x^2} \Rightarrow y' = 1 - 2x = 0 \Leftrightarrow x = \frac{1}{2}\)
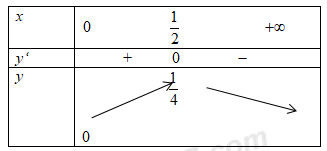
Xét \(y = - {x^2} + 5x - 4 \Rightarrow y' = - 2x + 5 = 0 \Leftrightarrow x = \frac{5}{2}\)
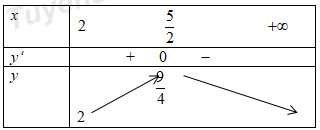
Để phương trình có 3 nghiệm thì \(0 \le m < \frac{1}{4}\)
Chọn B.
Đề thi giữa HK2 môn Toán 12 năm 2023-2024
Trường THPT Võ Văn Kiệt











