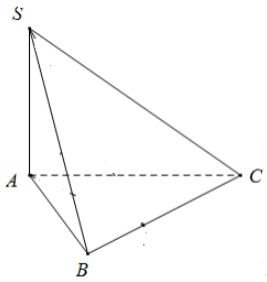
Cho hình chóp S.ABC có cạnh bên SA vuông góc với mặt đáy; \(BC = 9m,AB = 10m,AC = 17m\). Biết thể tích khối chóp S.ABC bằng 73m³. Tính khoảng cách h từ điểm A đến mặt phẳng (SBC). 

Câu hỏi liên quan

• Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình \({x^3} + {x^2} + x = m{\left( {{x^2} + 1} \right)^2}\) có nghiệm thuộc đoạn [0;1]. 

• Cho hàm số \(y = {x^3} - 4{x^2} + 5x - 2\). Mệnh đề nào sau đây đúng ? 

• Một công ti quản lí chuẩn bị xây dựng một khu chung cư mới. Họ tính toán nếu tòa nhà có x căn hộ thì chi phí bảo trì của tòa nhà là: C(x) = 4000 - 14x + 0,04x². Khu đất của họ có thể xây được tòa nhà chứa tối đa 300 căn hộ. Hỏi họ nên xây dựng tòa nhà có bao nhiêu căn hộ để chi phí bảo trì của tòa nhà là nhỏ nhất?

ZUNIA12

• Cho hình chóp S.ABC có đáy là tam giác vuông cân có cạnh huyền là 4a và thể tích bằng \(a^3\). Tính chiều cao h của khối chóp S.ABC. 

• Cho hình chóp S.ABCD có đáy là hình bình hành, gọi M là trung điểm của SC, mặt phẳng đi qua AM và song song với BD cắt SB, SD lần lượt tại N và P. Tính tỉ số k giữa thể tích hình chóp S.ANMP và thể tích hình chóp S.ABCD. 

• Cho hàm số y=f(x) có \(\mathop {\lim }\limits_{x \to  + \infty } f(x) = 1;\mathop {\lim }\limits_{x \to  - \infty } f(x) = 1\)Trong các khẳng định dưới đây, khẳng định nào là đúng? 

• Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh bằng a, góc \(\widehat{A}\)  bằng 600 và cạnh bên AA’ = 2a. Tính thể tích V của khối hộp ABCD.A’B’C’D’. 

•  Biết thể tích của khối lăng trụ ABC.A'B'C' bằng V. Tính thể tích \(V_1\) tứ diện A'ABC' theo V.

• Cho hàm số \(y = \frac{{ax + 1}}{{bx - 2}}.\) Xác định a và b để đồ thị hàm số nhận đường thẳng x=1 là tiệm cận đứng và đường thẳng \(y=\frac{1}{2}\) làm tiệm cận ngang. 

• Cho hàm số \(y = {x^3} - 3{x^2} + 3\) xác định trên [1;3]. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số thì M+m bằng : 

• Hàm số nào sau đây có đồ thị nhận đường thẳng x = 0 làm tiệm cận đứng? 

• Cho hàm số \(y = {x^3} - 2{{\rm{x}}^2} + x + 1\). Mệnh đề nào sau đây là đúng?

• Khối 12 mặt đều có bao nhiêu đỉnh?

• Cho hàm số \(y = \frac{{2x + \sqrt {{x^2} - 4} }}{{x - 2}}\) có đồ thị (C). Chọn mệnh đề đúng trong các mệnh đề sau: 

• Tìm tất cả các giá trị nguyên của tham số thực m để hàm số \(y = \frac{1}{3}{x^3} + \frac{1}{2}m{x^2}\) có điểm cực đại x1 điểm cực tiểu x² sao cho \(- 2 < {x_1} < - 1;\,\,1 < {x_2} < 2.\) 

• Cho hàm số y=f(x) xác định, liên tục trên R và có bảng biến thiên 

  

• Trong các mệnh đề sau, mệnh đề nào đúng?Cho hình đa diện (H) có các mặt là nhứng tam giác, mỗi đỉnh là đỉnh chung của đúng 3 mặt. Gọi số các đỉnh, cạnh, mặt của hình đa diện (H) lần lượt là d, c, m. Khi đó: 

• Đường tiệm cận đứng của đồ thị hàm số \(y = \frac{{\sqrt x }}{{4 - {x^2}}}\) là: 

• Đường tiệm cận ngang của đồ thị hàm số \(y = x + \sqrt {{x^2} + 2x} \) là:

• Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số \(y = \frac{{x - 1}}{{{x^2} - mx + m}}\) có đúng một tiệm cận đứng.