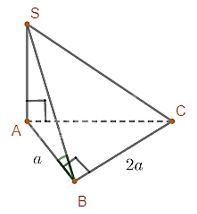
Cho khối chóp \(S.ABC\) có \(SA\) vuông góc với đáy, tam giác \(ABC\) vuông tại \(B\), \(AB = a,BC = 2a\), góc giữa \(\left( {SBC} \right)\) và mp đáy bằng \(30^\circ \). Khi đó thể tích khối chóp đã cho là?

Câu hỏi liên quan

• Có bao nhiêu giá trị thực của tham số \(m\) để pt \(m{.2^{{x^2} - 3x + 2}} + {2^{4 - {x^2}}} = {2^{6 - 3x}} + m\) có đúng \(3\) nghiệm thực phân biệt?

• Hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\). Cạnh bên \(SA\) vuông góc với đáy có độ dài bằng \(a\). Thể tích khối tứ diện \(S.BCD\) là?

• Tìm \(b\) để ĐTHS \(y = 2{x^4} + b{x^2} + 1\) có \(3\) cực trị?

ZUNIA12

• Cho hàm số \(y = f\left( x \right)\), hàm số \(f'\left( x \right) = {x^3} + a{x^2} + bx + c\,\,\)\(\left( {a,b,c \in \mathbb{R}} \right)\) có đồ thị như hình:

   

  Hàm số \(g\left( x \right) = f\left( {f'\left( x \right)} \right)\) nghịch biến trên khoảng nào?

• Giải phương trình sau \(\log \left( {x + 1} \right) + \log \left( {x + 3} \right) = \log \left( {x + 7} \right)\)?

• Đồ thị trong hình sau đây là của hàm số nào?

  

• Nghiệm của BPT \({\log _2}\left( {{{7.10}^x} - {{5.25}^x}} \right) > 2x + 1\) là?

• Cho hình nón \(\left( N \right)\) có đường sinh bằng \(9cm\), chiều cao bằng \(3cm\). Thể tích của hình nón \(\left( N \right)\) là bao nhiêu?

• Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), \(SA\) vuông góc với đáy, thể tích khối chóp \(S.ABCD\) bằng \(\dfrac{{2{a^3}}}{3}\). Tính k/c từ \(A\) đến mp \(\left( {SBD} \right)\)?

• Đường thẳng \(y = m\) và đường cong \(y =  - {x^4} + 4{x^2} + 2\) có 4 điểm chung khi nào?

• Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên:

   

  Hàm số đã cho đồng biến trên khoảng nào?

• Phương trình \({\log _3}\left( {{{3.2}^x} - 1} \right) - 2x - 1 = 0\) tương đương với phương trình nào dưới đây? 

• Khối chóp tứ giác đều có mặt đáy là hình gì?

• Tập nghiệm của pt \({\log _2}x = 5\) là? 

• Cho \(a\) là số thực dương khác \(1\). Mệnh đề nào bên dưới đây đúng với mọi số thực dương \(x,y\)? 

• Cho hàm số \(y = \dfrac{{3x - 1}}{{x - 3}}\,\,\left( C \right)\). Gọi \(M\) là điểm bất kì trên \(\left( C \right)\), \(d\) là tổng khoảng cách từ \(M\) đến 2 đường tiệm cận của đồ thị \(\left( C \right)\). GTNN của \(d\) là?

• Rút gọn biểu thức sau \(Q = {b^{\frac{5}{3}}}:\sqrt[3]{b}\) với \(b > 0\)? 

• Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\). Khi tăng cạnh của hình lập phương lên \(5\) lần thì ta được thể tích của hình lập phương mới là bao nhiêu?

• Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình:

   

  Tất cả các giá trị của tham số \(m\) để hàm số \(y = \left| {f\left( x \right) - m} \right|\) có ba điểm cực trị là?

• Nếu HS \(y = f\left( x \right)\) liên tục và đồng biến trên khoảng \(\left( { - 1;2} \right)\) thì hàm số \(y = f\left( {x + 2} \right)\) đồng biến trên khoảng nào?