Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, góc giữa mặt bên và mặt đáy bằng \({45^0}\). Thể tích khối chóp đã cho bằng?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai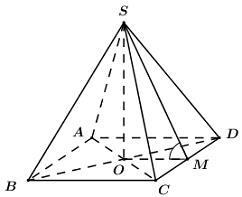
Gọi \(O = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right)\).
Gọi M là trung điểm của CD ta có:
\(\left\{ {\begin{array}{*{20}{l}}{CD \bot OM}\\{CD \bot SO}\end{array}} \right. \Rightarrow CD \bot \left( {SOM} \right) \Rightarrow CD \bot SM\).
\(\left\{ {\begin{array}{*{20}{l}}{\left( {SCD} \right) \cap \left( {ABCD} \right) = CD}\\{SM \subset \left( {SCD} \right),{\mkern 1mu} {\mkern 1mu} SM \bot CD}\\{OM \subset \left( {ABCD} \right),{\mkern 1mu} {\mkern 1mu} OM \bot CD}\end{array}} \right.\)\( \Rightarrow \angle \left( {\left( {SCD} \right);\left( {ABCD} \right)} \right) = \angle \left( {SM;OM} \right) = \angle SMO = {45^0}\).
\( \Rightarrow \Delta SOM\) vuông cân tại O \( \Rightarrow SO = OM = \dfrac{1}{2}AD = a\).
Vậy \({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}.a.{\left( {2a} \right)^2} = \dfrac{{4{a^3}}}{3}\).
Chọn B.
Đề thi giữa HK1 môn Toán 12 năm 2023-2024
Trường THPT Trần Hữu Trang