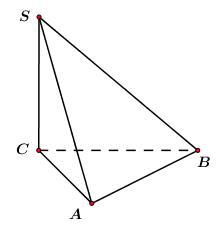
Cho lăng trụ tam giác đều \(ABC.A'B'C'\) có \(AB = a\), \(AA' = a\sqrt 2 .\) Khoảng cách giữa A'B và CC' bằng?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai
Ta có \(CC'//AA' \Rightarrow CC'//\left( {ABB'A'} \right)\)
Nên \(d\left( {CC';AB'} \right) = d\left( {CC';\left( {ABB'A'} \right)} \right) = d\left( {C;\left( {ABB'A'} \right)} \right)\)
Lấy \(H\) là trung điểm của AB
Khi đó \(CH \bot AB\) (do tam giác ABC đều)
Lại có \(AA' \bot CH\left( {do{\mkern 1mu} AA' \bot \left( {ABC} \right)} \right)\)
Nên \(CH \bot \left( {ABB'A'} \right)\) tại \(H \Rightarrow d\left( {C;\left( {ABB'A'} \right)} \right) = CH\)
Ta có \(CH = \dfrac{{a\sqrt 3 }}{2}\) (đường trung tuyến trong tam giác đều cạnh \(a\) )
Vậy \(d\left( {AB';CC'} \right) = \dfrac{{a\sqrt 3 }}{2}.\)
Chọn A.
Đề thi giữa HK1 môn Toán 12 năm 2023-2024
Trường THPT Trần Hữu Trang