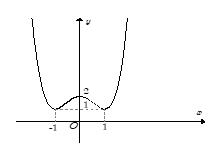
Số tiếp tuyến của đồ thị hàm số \(y = {x^4} - 2{x^2} - 3\) song song với trục hoành là?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiPhương pháp giải:
Tìm số nghiệm của phương trình \(y' = 0\).
Lời giải chi tiết:
Phương trình trục hoành: \(y = 0\).
Ta có \(y' = 4{x^3} - 4x \Rightarrow \) Hệ số góc của tiếp tuyến tại điểm có hoành độ \(x = {x_0}\) là \(y'\left( {{x_0}} \right) = 4x_0^3 - 4{x_0}\).
Tiếp tuyến // Ox \( \Rightarrow y'\left( {{x_0}} \right) = 0 \Leftrightarrow 4x_0^3 - 4{x_0} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{x_0} = 0}\\{{x_0} = {\rm{\;}} \pm 1}\end{array}} \right.\).
Khi \(x = \pm 1\) ta tìm được hai tiếp tuyến trùng nhau là \(y = - 3\)
Vậy có hai tiếp tuyến song song với trục hoành.
Chọn C.
Đề thi giữa HK1 môn Toán 12 năm 2023 - 2024
Trường THPT Bắc Ninh