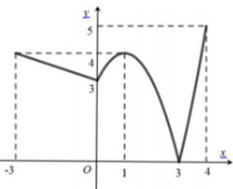
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 3;4} \right]\) và có đồ thị như hình vẽ bên. Gọi \(M\) và \(m\) lần lượt là các giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn \(\left[ { - 3;4} \right]\). Tính \(M + m\)?

Câu hỏi liên quan

• Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:

  

  Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

• Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( x \right) = 2{x^3} + 3{x^2} - 1\) trên đoạn\(\left[ { - 2; - \dfrac{1}{2}} \right]\). Tính \(P = M - m\)?

• Số đường tiệm cận của đồ thị hàm số \(y = \dfrac{{x + 1 - \sqrt {3x + 1} }}{{{x^2} - 3x + 2}}\) là?

ZUNIA12

• Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {\left( {x + 1} \right)^2}\left( {2 - x} \right)\left( {x + 3} \right).\) Mệnh đề nào dưới đây đúng?

• Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\left( {a;b} \right)\). Phát biểu nào sau đây là sai?

• Gọi I là tâm đối xứng của đồ thị hàm số \(y = \dfrac{{2x - 3}}{{x + 2}}\). Tìm tọa độ điểm \(I\)?

• Gọi \(A\left( {{x_1};{y_1}} \right)\), \(B\left( {{x_2};{y_2}} \right)\) là hai điểm cực trị của đồ thị hàm số \(y = {x^3} - 3x - 2\). Giá trị \({y_1} + {y_2}\) bằng?

• Số giao điểm của đồ thị hàm số \(y = {x^4} - 2{x^2} + 1\) và đường thẳng \(y = 1\) là?

• Đồ thị sau đây là của hàm số \(y = {x^4} - 3{x^2} - 3.\) Với giá trị nào của m thì phương trình \({x^4} - 3{x^2} - 3 = m\) có đúng 3 nghiệm phân biệt?

  

• Xét các khẳng định sau:

  i) Nếu hàm số \(y = f\left( x \right)\) có đạo hàm cấp hai trên \(\mathbb{R}\)và đạt cực tiểu tại \(x = {x_0}\) thì \(\left\{ {\begin{array}{*{20}{l}}{f'({x_0}) = 0}\\{f''({x_0}) > 0}\end{array}} \right.\)

  ii) Nếu hàm số \(y = f\left( x \right)\) có đạo hàm cấp hai trên \(\mathbb{R}\)và đạt cực đại tại \(x = {x_0}\) thì \(\left\{ {\begin{array}{*{20}{l}}{f'({x_0}) = 0}\\{f''({x_0}) < 0}\end{array}} \right.\)

  iii) Nếu hàm số \(y = f\left( x \right)\) có đạo hàm cấp hai trên \(\mathbb{R}\) và \(f''({x_0}) = 0\)thì hàm số không đạt cực trị tại \(x = {x_0}\)

  Số khẳng định đúng trong các khẳng định trên là?

• Cho hình chóp S.ABC có đáy ABC vuông tại A và SB vuông góc với đáy. Biết \(SB = a\) và SC hợp với (SAB) một góc 300 và (SAC) hợp với (ABC) một góc 600. Thể tích khối chóp là?

• Tìm giá trị nhỏ nhất của hàm số \(y = \dfrac{{{x^2} - 5}}{{x + 3}}\) trên \(\left[ {0;2} \right]?\)

• Khẳng định nào dưới đây về hàm số \(y = {\rm{\;}} - {x^4} - 3{x^2} + 2\) là đúng?

• Cho hình chóp đều S.ABC có độ dài cạnh đáy là 2a, mặt bên tạo với mặt đáy một góc \({60^0}\). Tính thế tích của khối chóp S.ABC?

• Cho hình chóp S.ABC có đáy là tam giác vuông tại B, cạnh bên SA vuông góc với mặt phẳng đáy, \(AB = 2a,{\mkern 1mu} {\mkern 1mu} \widehat {BAC} = {60^0}\) và \(SA = a\sqrt 2 .\) Góc giữa đường thẳng SB và mặt phẳng \(\left( {SAC} \right)\) bằng?

• Cho hình chóp S.ABCD có đáy là hình thoi cạnh \(a\), \(\angle BAD = {60^0}\), cạnh bên \(SA = a\) và SA vuông góc với mặt phẳng đáy. Tính khoảng cách từ \(B\) đến mặt phẳng \(\left( {SCD} \right)\)?

  Câu 26: Cho hàm số \(y = \dfrac{{x + 3}}{{ - 1 - x}}\). Tìm mệnh đề đúng trong các mệnh đề sau:

  A. Hàm số nghịch biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\).

  B. Hàm số đồng biến trên các khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\).

  C. Hàm số đồng biến trên \(\mathbb{R}\backslash \left\{ 1 \right\}\).

  D. Hàm số đồng biến trên \(\left( {2; + \infty } \right)\).

• Đồ thị hàm số \(y = \dfrac{x}{{\sqrt {{x^2} - 1} }}\) có bao nhiêu đường tiệm cận?

• Đồ thị hình bên là của hàm số nào?

  

• Đồ thị trong hình vẽ dưới đây là đồ thị của hàm số nào?

  

• Cho hàm số \(y = \dfrac{{x + 3}}{{ - 1 - x}}\). Tìm mệnh đề đúng trong các mệnh đề sau?