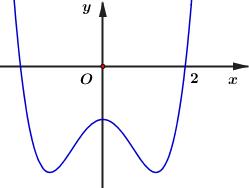
Khẳng định nào dưới đây về hàm số \(y = {\rm{\;}} - {x^4} - 3{x^2} + 2\) là đúng?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiPhương pháp giải:
Điểm \({x_0}\) được gọi là điểm cực đại của hàm số \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{y'\left( {{x_0}} \right) = 0}\\{y''\left( {{x_0}} \right) < 0}\end{array}} \right.\)
Điểm \({x_0}\) được gọi là điểm cực tiểu của hàm số \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{y'\left( {{x_0}} \right) = 0}\\{y''\left( {{x_0}} \right) > 0}\end{array}} \right.\)
Lời giải chi tiết:
\(\begin{array}{*{20}{l}}{TXD:{\mkern 1mu} {\mkern 1mu} D = R}\\{y' = {\rm{\;}} - 4{x^3} - 6x = 0 \Leftrightarrow x = 0}\\{y'' = {\rm{\;}} - 12x - 6 \Rightarrow y''\left( 0 \right) = {\rm{\;}} - 6 < 0}\end{array}\)
\( \Rightarrow \) Hàm số đạt cực đại tại \(x = 0\) và không có cực tiểu.
Chọn B.
Đề thi giữa HK1 môn Toán 12 năm 2023 - 2024
Trường THPT Bắc Ninh
.jpg)











