220 câu trắc nghiệm Lý thuyết điều khiển tự động
Với hơn 220 câu trắc nghiệm Lý thuyết điều khiển tự động được chia sẻ dành cho các bạn sinh viên chuyên ngành tham khảo ôn tập chuẩn bị cho kì thi sắp tới. Bộ câu hỏi xoay quanh những kiến thức về các phương pháp nghiên cứu hệ thống tự động, bao gồm các phương pháp thiết lập mô hình toán của hệ thống, phân tích – đánh giá chất lượng hệ thống cũng như thiết kế bộ điều khiển...Để việc ôn tập trở nên hiệu quả hơn, các bạn có thể ôn theo từng phần trong bộ câu hỏi này bằng cách trả lời lần lượt các câu hỏi cũng như so sánh đáp và lời giải chi tiết được đưa ra. Sau đó các bạn hãy chọn tạo ra đề ngẫu nhiên để kiểm tra lại kiến thức mình đã ôn tập được nhé!
Chọn hình thức trắc nghiệm (25 câu/30 phút)
Chọn phần
-
Câu 1:
G(jω)=P(ω)+jQ(ω)=M(ω)ejφ(ω), trong đó:
A. M(ω) là đáp ứng pha, φ(ω) là đáp ứng biên độ
B. M(ω) là độ lợi, ω là tần số cắt
C. M(ω) là đáp ứng biên độ, φ(ω) là đáp ứng pha
D. P(ω) là pha của hệ thống
-
Câu 2:
Hàm truyền vòng kín của hệ thống hồi tiếp dương là:
A. \(\frac{{G(s)}}{{1 - G(s)H(s)}}\)
B. \(\frac{{G(s)}}{{1 + H(s)}}\)
C. \(\frac{1}{{1 + G(s)H(s)}}\)
D. \(\frac{{G(s)}}{{1 + G(s)}}\)
-
Câu 3:
Cho hệ có phương trình đặc trưng. Xét tính ổn định của hệ thống, và cho biết có bao nhiêu nghiệm có phần thực dương:
A. Hệ thống không ổn định, có 2 nghiệm có phần thực dương
B. Hệ thống không ổn định, có 3 nghiệm có phần thực dương
C. Hệ thống không ổn định, có 1 nghiệm có phần thực dương
D. Hệ thống ổn định, có 4 nghiệm nằm bên trái mặt phẳng phức
-
Câu 4:
: Biến đổi Laplace của hàm nấc đơn vị (step) f(t)=1(t):
A. s2
B. 1/s
C. a
D. s
-
Câu 5:
Cho hệ có phương trình đặc trưng s3+(K+2)s2+2Ks+10=0 . Hãy xác định K để hệ thống ổn định:
A. K >-2
B. K >0
C. K >1,45
D. K >2
-
Câu 6:
Cho phương trình 2s4+s3+3s2+5s+10=0 .Xét tính ổn định của hệ thống, và cho biết có bao nhiêu nghiệm có phần thực dương:
A. Hệ thống ổn định, có 4 nghiệm nằm bên trái mặt phẳng phức
B. Hệ thống không ổn định, có 3 nghiệm bên phải mặt phẳng phức, 1 nghiệm bên trái mặt phẳng phức
C. Hệ thống không ổn định, có 2 nghiệm bên phải mặt phẳng phức, 2 nghiệm bên trái mặt phẳng phức
D. Hệ thống không ổn định, có 1 nghiệm bên phải mặt phẳng phức, 3 nghiệm bên trái mặt phẳng phức
-
Câu 7:
Sơ đồ khối hệ thống điều khiển vòng kín gồm có các phần tử cơ bản sau:
A. Tín hiệu vào, tín hiệu ra
B. Các khối hàm truyền đạt mắc nối tiếp
C. Thiết bị điều khiển, các bộ điều khiển , vòng hồi tiếp
D. Các khối hàm truyền đạt mắc song song
-
Câu 8:
Điều kiện cần để hệ thống liên tục ổn định theo tiêu chuẩn ổn định đại số là:
A. Tất cả các hệ số của phương trình đặc trưng phải khác không và cùng dấu
B. Tất cả các hệ số của phương trình đặc trưng phải khác không
C. Tất cả các hệ số của phương trình đặc trưng phải cùng dấu
D. Tất cả các hệ số của phương trình đặc trưng phải dương
-
Câu 9:
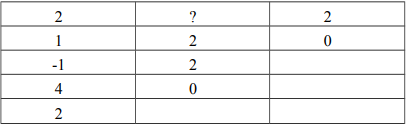
Cho hệ thống có phương trình đặc trưng: 2s4 +s3 + 3s2 + 2s + 2 = 0 . Bảng Routh của hệ thống được cho như sau:
Phần tử “?” có giá trị bằng:
A. 2
B. 3
C. 4
D. 5
-
Câu 10:
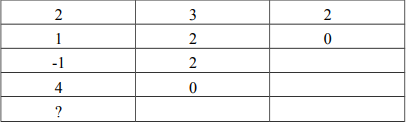
Cho hệ thống có phương trình đặc trưng: 2s4 +s3 + 3s2 + 2s + 2 = 0 . Bảng Routh của hệ thống được cho như sau:
Phần tử “?” có giá trị bằng:
A. 2
B. 3
C. 4
D. 5
-
Câu 11:
Hàm truyền đạt \(G(s) = \frac{{{V_o}(s)}}{{{V_i}(s)}}\) của mạch điện ở hình sau là:
.png)
A. \(\frac{{{R_2}}}{{{R_1}}} + {R_2}Cs\)
B. \(- \frac{{{R_2}}}{{{R_1}}} - {R_2}Cs\)
C. \(\frac{{{R_2}}}{{{R_1}}} - {R_2}Cs\)
D. \(\frac{{{R_2}}}{{{R_1}}} + {R_2}Cs\)
-
Câu 12:
Cho hàm truyền \(G(s) = \frac{5}{{{s^3} + 8{s^2} + 9s + 2}}\) hãy lập phương trình trạng thái:
A. \(A = \left[ {\begin{array}{*{20}{c}} 0&1&0\\ 0&0&1\\ { - 2}&{ - 9}&{ - 8} \end{array}} \right]{\rm{ ; B = }}\left[ \begin{array}{l} 0\\ 0\\ 5 \end{array} \right]{\rm{ ; C = }}\left[ {1{\rm{ 0 0}}} \right];\)
B. \(A = \left[ {\begin{array}{*{20}{c}} 0&1&0\\ 0&0&1\\ 2&9&8 \end{array}} \right]{\rm{ ; B = }}\left[ \begin{array}{l} 0\\ 0\\ 5 \end{array} \right]{\rm{ ; C = }}\left[ {1{\rm{ 0 0}}} \right];\)
C. \(A = \left[ {\begin{array}{*{20}{c}} 0&1&0\\ 0&0&1\\ { - 2}&{ - 9}&{ - 8} \end{array}} \right]{\rm{ ; B = }}\left[ \begin{array}{l} 0\\ 0\\ 2 \end{array} \right]{\rm{ ; C = }}\left[ {1{\rm{ 1 0}}} \right];\)
D. \(A = \left[ {\begin{array}{*{20}{c}} 1&1&0\\ 0&0&1\\ { - 2}&{ - 9}&{ - 8} \end{array}} \right]{\rm{ ; B = }}\left[ \begin{array}{l} 0\\ 1\\ 2 \end{array} \right]{\rm{ ; C = }}\left[ {1{\rm{ 0 0}}} \right];\)
-
Câu 13:
Đặc tính tần số của hệ thống là:
A. Tỉ số giữa tín hiệu vào xác lập và tín hiệu ra hình sin
B. Là tỉ số giữa tín hiệu vào hình sin và tín hiệu ra xác lập
C. Là tỉ số giữa tín hiệu ra hình sin và tín hiệu vào xác lập
D. Tỉ số giữa tín hiệu ra ở trạng thái xác lập và tín hiệu vào hình sin
-
Câu 14:
Cho hàm truyền ,hãy lập phương trình trạng thái:
A. \(A = \left[ {\begin{array}{*{20}{c}} 0&1&0\\ 0&{ - 2}&1\\ 0&0&{ - 3} \end{array}} \right]{\rm{ ; B = }}\left[ \begin{array}{l} 0\\ 0\\ 6 \end{array} \right]{\rm{ ; C = }}\left[ {1{\rm{ 0 0}}} \right];\)
B. \(A = \left[ {\begin{array}{*{20}{c}} 0&1&0\\ 0&0&1\\ { - 6}&{ - 11}&{ - 6} \end{array}} \right]{\rm{ ; B = }}\left[ \begin{array}{l} 0\\ 0\\ 6 \end{array} \right]{\rm{ ; C = }}\left[ {1{\rm{ 0 0}}} \right];\)
C. \(A = \left[ {\begin{array}{*{20}{c}} 0&1&0\\ 0&0&1\\ 6&{11}&6 \end{array}} \right]{\rm{ ; B = }}\left[ \begin{array}{l} 0\\ 0\\ 6 \end{array} \right]{\rm{ ; C = }}\left[ {1{\rm{ 0 0}}} \right];\)
D. \(A = \left[ {\begin{array}{*{20}{c}} { - 1}&1&0\\ 0&0&1\\ 6&{11}&6 \end{array}} \right]{\rm{ ; B = }}\left[ \begin{array}{l} 0\\ 3\\ 6 \end{array} \right]{\rm{ ; C = }}\left[ {1{\rm{ 0 0}}} \right];\)
-
Câu 15:
Hàm truyền của hiệu chỉnh vi phân tỉ lệ PD (proportional derivative) liên tục có dạng:
A. \({G_C}(s) = {K_p} + {K_D}\)
B. \({G_C}(s) = {K_p} + {K_D}s\)
C. \({G_C}(s) = {K_p}s + {K_D}\)
D. \({G_C}(s) = {K_p} + \frac{{{K_D}}}{s}\)
-
Câu 16:
Hệ thống rời rạc bậc n được mô tả bằng:
A. Phương trình vi phân bậc n
B. Phương trình sai phân bậc n
C. (n+1) biến trạng thái
D. (n-1) biến trạng thái
-
Câu 17:
Hệ MIMO là hệ thống có:
A. Nhiều ngõ vào- nhiều ngõ ra
B. Nhiều ngõ vào - một ngõ ra
C. Một ngõ vào – một ngõ ra
D. Một ngõ vào – nhiều ngõ ra
-
Câu 18:
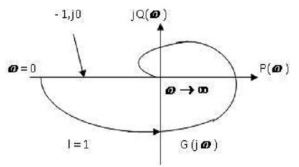
Cho hệ thống hở có đặc tính tần số như hình vẽ . Xét tính ổn định của hệ thống:
A. Hệ thống ở biên giới ổn định
B. Hệ thống không ổn định
C. Hệ thống ổn định
D. Đường cong Nyquist bao điểm (1,j0) 2 vòng theo chiều dương
-
Câu 19:
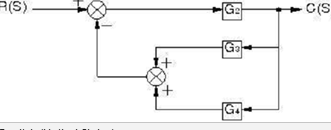
Hàm truyền \(G(s) = \frac{{C(s)}}{{R(s)}}\) của hệ thống ở hình trên là:
A. \(\frac{{{G_2}}}{{1 + {G_2}({G_3} - {G_4})}}\)
B. \(\frac{{{G_2}}}{{1 + {G_2}({G_3} + {G_4})}}\)
C. \(\frac{{{G_2}}}{{1 - {G_2}({G_3} + {G_4})}}\)
D. \(\frac{{{G_2}}}{{1 - {G_2}({G_3} - {G_4})}}\)
-
Câu 20:
Hàm truyền vòng kín của hệ thống hồi tiếp âm đơn vị là:
A. \({G_k}(s) = \frac{{G(s)}}{{1 + G(s)H(s)}}\)
B. \({G_k}(s) = \frac{{G(s)}}{{1 - G(s)}}\)
C. \({G_k}(s) = \frac{{G(s)H(s)}}{{1 - G(s)}}\)
D. \({G_k}(s) = \frac{{G(s)}}{{1 + G(s)}}\)
-
Câu 21:
Hàm truyền vòng kín của hệ thống hồi tiếp dương đơn vị là:
A. \({G_k}(s) = \frac{{G(s)}}{{1 + G(s)H(s)}}\)
B. \({G_k}(s) = \frac{{G(s)}}{{1 - G(s)}}\)
C. \({G_k}(s) = \frac{{G(s)H(s)}}{{1 - G(s)}}\)
D. \({G_k}(s) = \frac{{G(s)}}{{1 + G(s)}}\)
-
Câu 22:
Cho phương trình \({s^2} + 25{s^2} + 250s + 10 = 0\). Xét tính ổn định của hệ thống, và cho biết có bao nhiêu nghiệm có phần thực dương:
A. Hệ thống ổn định, không có nghiệm có phần thực dương
B. Hệ thống không ổn định, có 3 nghiệm bên phải mặt phẳng phức
C. Hệ thống không ổn định, có 2 nghiệm bên phải mặt phẳng phức, 1 nghiệm bên trái mặt phẳng phức
D. Hệ thống không ổn định, có 1 nghiệm bên phải mặt phẳng phức, 2 nghiệm bên trái mặt phẳng phức
-
Câu 23:
Hàm truyền của hiệu chỉnh tỉ lệ P (proportional) liên tục có dạng:
A. \({G_C}(s) = {K_p} + {K_D}s\)
B. \({G_C}(s) = {K_p}s + {K_D}\)
C. \({G_C}(s) = {K_p} + \frac{{{K_D}}}{s}\)
D. \({G_C}(s) = {K_p}\)
-
Câu 24:
Hệ phương trình trạng thái được mô tả dưới dạng ma trận, với:
\(\left\{ \begin{array}{l} x(t) = A(x) + Br(t)\\ C(t) = Cx(t) \end{array} \right.\)
A. A là ma trân {1 x n}
B. A là ma trận {n x 1}
C. A là ma trận vuông {n x n}
D. A là ma trận {n x m}, với n khác m
-
Câu 25:
Các trạng thái cân bằng gồm:
A. Biên giới ổn định, ổn định
B. Ổn định, không ổn định
C. Biên giới ổn định, ổn định, không ổn định
D. Biên giới ổn định, không ổn định