Cho các số phức \(w,\,z\) thỏa mãn \(\left| w+i \right|=\frac{3\sqrt{5}}{5}\) và \(5w=\left( 2+i \right)\left( z-4 \right)\). Giá trị lớn nhất của biểu thức \(P=\left| z-1-2i \right|+\left| z-5-2i \right|\) bằng
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai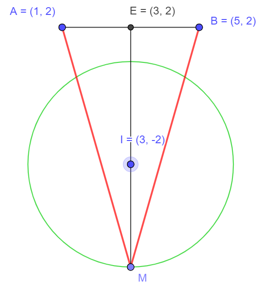
Gọi \(z=x+yi\,\,\left( x,\,y\in \mathbb{R} \right)\) khi đó \(M\left( x;\,y \right)\) biểu diễn cho số phức \(z\).
Theo đề bài: \(5w=\left( 2+i \right)\left( z-4 \right)\)
\(\begin{align} & \Leftrightarrow 5\left( w+i \right)=\left( 2+i \right)z-\left( 8-i \right)\\ &\Leftrightarrow \left| 5\left( w+i \right) \right|=\left| \left( 2+i \right)z-\left( 8-i \right) \right| \\ & \Leftrightarrow \left| \left( 2-i \right)\left( w+i \right) \right|=\left| z-\left( 3-2i \right) \right|\\ &\Leftrightarrow \left| z-\left( 3-2i \right) \right|=3. \\ \end{align}\)
Suy ra \(M\left( x;\,y \right)\) thuộc đường tròn tâm \(I\left( 3;\,-2 \right)\) và bán kính \(R=3\).
Ta có \(P=\left| z-1-2i \right|+\left| z-5-2i \right|=\left| z-\left( 1+2i \right) \right|+\left| z-\left( 5+2i \right) \right|=MA+MB\) với \(A\left( 1;\,2 \right)\) và \(B\left( 5;\,2 \right)\).
Gọi \(E\) là trung điểm của đoạn thẳng \(AB\) suy ra \(E\left( 3;\,2 \right)\) và \(IE=4\) (\(E\)nằm ngoài \(\left( I \right)\)).
\(P=MA+MB\le \sqrt{\left( {{1}^{2}}+{{1}^{2}} \right)\left( M{{A}^{2}}+M{{B}^{2}} \right)}\)\( =\sqrt{2\left( M{{A}^{2}}+M{{B}^{2}} \right)}\)\( =\sqrt{4M{{E}^{2}}+A{{B}^{2}}}\)\( =\sqrt{4M{{E}^{2}}+16}\).
Biểu thức \(P\)đạt giá trị lớn nhất khi độ dài \(ME\) lớn nhất hay \(M,\,I,\,E\) thẳng hàng.
Khi đó \(M{{E}_{\max }}=IE+IM=7\) và \(\overrightarrow{IM}=\frac{3}{4}\overrightarrow{EI}\Rightarrow M\left( 3;-5 \right)\).
Vậy biểu thức \({{P}_{\max }}=\sqrt{{{4.7}^{2}}+16}=2\sqrt{53}\) khi \(z=3-5i\) và \(w=\frac{3}{5}-\frac{11}{5}i\).
Đề thi thử tốt nghiệp THPT môn Toán năm 2023
Trường THPT Herman-Gmeiner