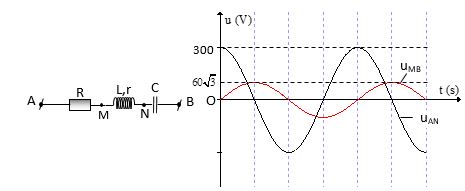
Cho đoạn mạch AB như hình vẽ. Biết R = 80 W, r = 20 W. Đặt vào hai đầu mạch một điện áp xoay chiều \(u\,=\,U\sqrt{2}\cos 100\pi t\text{ }(V).\) Đồ thị biểu diễn sự phụ thuộc của điện áp tức thời giữa hai điểm A, N (uAN) và giữa hai điểm M, B (uMB) theo thời gian được biểu diễn như hình vẽ.
Hệ số công suất của đoạn mạch AB có giá trị gần giá trị nào nhất sau đây?
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTừ đồ thị ta có:
\({{\overrightarrow{U}}_{AN}}\bot {{\overrightarrow{U}}_{MB}}\Leftrightarrow \tan {{\varphi }_{AN}}\tan {{\varphi }_{MB}}=-1\Leftrightarrow \frac{{{U}_{L}}}{{{U}_{R}}+{{U}_{r}}}.\frac{{{U}_{C}}-{{U}_{L}}}{{{U}_{r}}}=-1\) (1)
Và \(R=4r\Rightarrow {{U}_{R}}=4{{U}_{r}}\xrightarrow{(1)}{{\left( {{U}_{L}}-{{U}_{C}} \right)}^{2}}=\frac{25U_{r}^{4}}{U_{L}^{2}}\) (2)
Mặt khác:
\(\left\{ \begin{array}{l}
U_{AN}^2 = {\left( {{U_R} + {U_r}} \right)^2} + U_L^2\\
U_{MB}^2 = U_r^2 + {\left( {{U_L} - {U_C}} \right)^2}
\end{array} \right.\left\{ \begin{array}{l}
{\left( {150\sqrt 2 } \right)^2} = 25U_r^2 + U_L^2\\
{\left( {30\sqrt 6 } \right)^2} = U_r^2 + \frac{{25U_r^4}}{{U_L^2}}
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
{U_r} = 15\sqrt 6 V\\
{U_L} = 75\sqrt 2 V
\end{array} \right.\)
Suy ra:
\(\left\{ \begin{array}{l}
{U_R} = 60\sqrt 6 V\\
{U_C} = 120\sqrt 2 V
\end{array} \right. \Rightarrow \cos \varphi = \frac{{{U_R} + {U_r}}}{{\sqrt {{{\left( {{U_R} + {U_r}} \right)}^2} + {{\left( {{U_L} - {U_C}} \right)}^2}} }} = \frac{{5\sqrt 7 }}{{14}} = 0,945.\)
Câu hỏi liên quan
-
Để tăng dung kháng của một tụ điện phẳng có điện môi là không khí ta
-
Poloni \({}_{84}^{210}Po\) phóng xạ theo phương trình: \({}_{84}^{210}Po\to X+{}_{82}^{206}Pb\). Hạt X là
-
Hạt nhân \({}_{6}^{14}C\) phóng xạ \({{\beta }^{-}}\). Hạt nhân con sinh ra có
-
Trên một sợi dây đàn hồi rất dài có một sóng ngang hình sin truyền theo trục Ox. Hình ảnh của một đoạn dây có hai điểm M và N tại hai thời điểm \({{t}_{1}}\) và \({{t}_{2}}\) như hình vẽ. Biết \(\Delta t={{t}_{2}}-{{t}_{1}}=0,05s
.png)
-
Một con lắc lò xo dao động điều hòa theo phương thẳng đứng với tần số góc \(\omega =20rad/s\) tại vị trí có gia tốc trọng trường \(g=10m/{{s}^{2}}\). Khi qua vị trí x = 2cm, vật có vận tốc \(v=40\sqrt{3}cm/s\). Lực đàn hồi cực tiểu của lò xo trong quá trình dao động có độ lớn là
-
Đoạn mạch MN gồm các phần tử \(R=100\Omega \), \(L=\frac{2}{\pi }H\) và \(C=\frac{100}{\pi }\mu F\) ghép nối điện. Đặt điện áp \(u=220\sqrt{2}cos\left( 100\pi t-\frac{\pi }{4} \right)\)V vào hai đầu đoạn mạch MN. Cường độ dòng điện tức thời qua mạch có biểu thức là
-
Điện áp \(u={{U}_{0}}cos\left( 100\pi t \right)\) (t tính bằng s) được đặt vào hai đầu đoạn mạch gồm cuộn dây và tụ điện mắc nối tiếp. Cuộn dây có độ tự cảm \(L=\frac{0,15}{\pi }H\) và điện trở \(r=5\sqrt{3}\Omega \), tụ điện có điện dung \(C=\frac{{{10}^{-3}}}{\pi }F\). Tại thời điểm \({{t}_{1}}\)(s) điện áp tức thời hai đầu cuộn dây có giá trị 100 V, đến thời điểm \({{t}_{2}}={{t}_{1}}+\frac{1}{75}s\) thì điện áp tức thời hai đầu tụ điện cũng bằng 100 V. Gía trị của \({{U}_{0}}\) gần đúng là
-
Trong thí nghiệm Young về giao thoa ánh sáng có hai khe được chiếu bằng ánh sáng đơn sắc có bước sóng \(\lambda \). Nếu tại điểm M trên màn quan sát có vân tối thứ ba (tính từ vân sáng trung tâm) thì hiệu đường đi của ánh sáng từ hai khe \({{S}_{1}},{{S}_{2}}\) đến M có độ lớn bằng
-
Hai nguồn sóng kết hợp A, B trên mặt thoáng chất lỏng dao động theo phương vuông góc với bề mặt chất lỏng với phương trình \({{u}_{A}}={{u}_{B}}=4cos\left( 10\pi t \right)mm\). Coi biên độ sóng không đổi, tốc độ sóng
v = 15 cm/s. Hai điểm \({{M}_{1}},{{M}_{2}}\) cùng nằm trên một elip nhận A, B làm tiêu điểm có \(A{{M}_{1}}-B{{M}_{1}}=1cm\) và \(A{{M}_{2}}-B{{M}_{2}}=3,5cm\). Tại thời điểm li độ của M là 3mm thì li độ của M tại thời điểm đó là:
-
Một máy phát điện xoay chiều một pha có phần cảm là roto quay với tốc độ 750 vòng/phút. Tần số của suất điện động cảm ứng là 50 Hz. Số cặp cực của máy phát là
-
Phát biểu nào sau đây đúng khi nói về sóng điện từ?
-
Đặt điện áp xoay chiều vào hai đầu mạch RLC nối tiếp, cuộn dây thuần cảm. Khi nối tắt tụ C thì điện áp hiệu dụng hai đầu R tăng 3 lần và dòng điện trong hai trường hợp vuông pha nhau. Hệ số công suất của mạch sau khi nối tắt C là
-
Vật tham gia đồng thời vào 2 dao động điều hòa cùng phương cùng tần số \({{x}_{1}}={{A}_{1}}cos\omega t\) và \({{x}_{2}}={{A}_{2}}cos(\omega t-\frac{\pi }{2})\). Với \({{v}_{\text{max}}}\) là vận tốc cực đại của vật. Khi hai dao động thành phần \({{x}_{1}}={{x}_{2}}={{x}_{0}}\) thì \({{x}_{0}}\) bằng:
-
Một sóng truyền theo phương AB. Tại một thời điểm nào đó, hình dạng sóng có dạng như hình vẽ. Biết rằng điểm M đang đi lên vị trí cân bằng. Khi đó điểm N đang chuyển động
-
Một vật dao động điều hòa với phương trình dạng cosin. Chọn gốc tính thời gian khi vật đổi chiều chuyển động và khi đó gia tốc của vật đang có giá trị dương. Pha ban đầu là
-
Một dây dẫn tròn mang dòng điện 20A thì tâm vòng dây có cảm ứng từ \(0,4\pi \mu T\). Nếu dòng điện qua dây dẫn giảm 5A so với ban đầu thì cảm ứng từ tại tâm vòng dây là
-
Chiếu bức xạ có bước sóng 0,5 \(\mu m\) vào một tấm kim loại có công thoát 1,8 eV. Dùng màn chắn tách một chùm hẹp các electron quang điện và cho nó bay vào một điện trường từ A đến B sao cho \({{U}_{AB}}=-10,8V\). Vận tốc nhỏ nhất và lớn nhất của electron khi tới B lần lượt là
-
Phát biểu nào sau đây về mắt là đúng?
-
Trong thí nghiệm Young về giao thoa ánh sáng, khoảng cách giữa hai khe là 2 mm, khoảng cách từ hai khe đến màn là 2 m, ánh sáng đơn sắc dùng trong thí nghiệm có bước sóng trong khoảng từ \(0,40\mu m\) đến \(0,76\mu m\). Tại vị trí cách vân sáng trung tâm, 1,56 mm là một vân sáng. Bước sóng của ánh sáng dùng trong thí nghiệm là
-
Khi có sóng dừng trên một đoạn dây đàn hồi với hai điểm A,B trên dây là các nút sóng thì chiều dài AB sẽ
