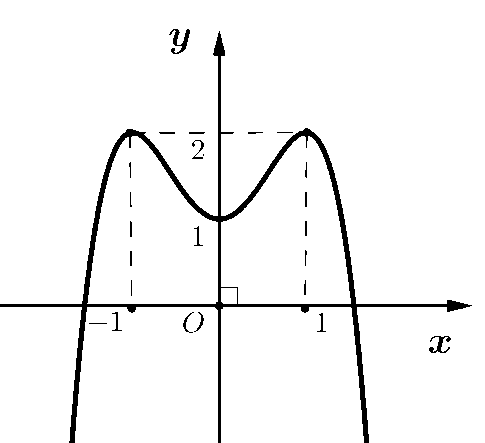
Cho hàm đa thức bậc ba \(y=f\left( x \right)\) liên tục, có đạo hàm trên \(\left[ -2;2 \right]\) và có đồ thị như hình:

 

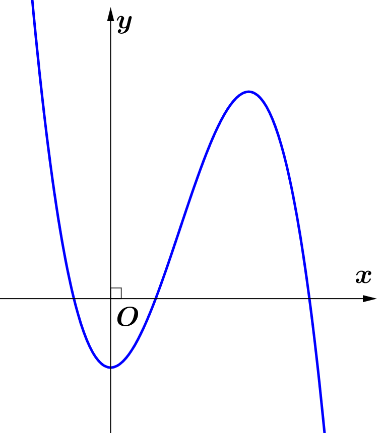
Số điểm cực tiểu của hàm số \(y=\sqrt[3]{{{\left( f\left( x \right) \right)}^{2}}}\) là?

Câu hỏi liên quan

• Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị \({f}'\left( x \right)\) như hình vẽ:

  

  Bất phương trình \({{\log }_{5}}\left[ f\left( x \right)+m+2 \right]+f\left( x \right)>4-m\) đúng với mọi \(x\in \left( -1\,;\,4 \right)\) khi và chỉ khi?

• Tính tổng \(T\) tất cả các nghiệm thực của phương trình sau \({{4.9}^{x}}-{{13.6}^{x}}+{{9.4}^{x}}=0\)?

• Đồ thị của hàm số nào bên dưới có dạng như đường cong trong hình?

  

ZUNIA12

• Trong không gian \(Oxyz\), mặt phẳng \((\alpha ):5x-7y-z+2=0\) nhận vectơ nào dưới đây làm vectơ pháp tuyến?

• Cho số phức \(z=-2+i\). Trong hình dưới đây, điểm biểu diễn số phức \(\overline{z}\) là?

  

• Phương trình sau \({{\log }_{2}}(x-5)=5\) có nghiệm là?

• Cho HS \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có \(f\left( -2 \right)=2;f\left( 0 \right)=1.\) Tính \(I=\int\limits_{-2}^{0}{\frac{{f}'\left( x \right)-f\left( x \right)}{{{e}^{x}}}dx}\)?

• Cho số phức \(z=1-2i\). Cho biết phần ảo của số phức \(\overline{z}\)?

• Cho HS \(y=f\left( x \right)\) liên tục trên đoạn \(\left[ a;b \right]\). Gọi \(D\) là hình phẳng giới hạn bởi ĐTHS \(y=f\left( x \right)\), trục hoành và 2 đường thẳng \(x=a,\ x=b\). Thể tích khối tròn xoay được tạo thành khi quay \(D\) quanh trục hoành được tính theo công thức?

• Tìm họ các nguyên hàm của hàm số sau \(y={{e}^{x}}+2x\)?

• Biết \(F(x)\) là một nguyên hàm của HS \(f(x)=\frac{1}{x}\) trên \(\left( 0;+\infty  \right)\) và \(F(1)=1\). Tính \(F(3)\)?

• Trong không gian \(Oxyz\), cho đường thẳng \(d\) có pt \(d:\,\left\{ \begin{align}
    & x=-1+t \\ 
   & y=2-3t \\ 
   & z=t \\ 
  \end{align} \right.\) và điểm \(A\left( 2;\,3;\,1 \right).\) Mặt phẳng \(\left( P \right)\) đi qua điểm \(A\), vuông góc với đường thẳng \(d\) có phương trình là?

• Trong không gian cho hình chữ nhật \(ABCD\) có \(AB=1\) và \(AD=2\). Gọi \(M,N\) lần lượt là trung điểm của \(AD\) và \(BC\). Quay hình chữ nhật đó xung quanh trục MN, ta được hình trụ. Tính diện tích toàn phần của hình trụ?

• Có bao nhiêu giá trị nguyên của tham số m để HS \(y=\frac{1}{3}{{x}^{3}}-m{{x}^{2}}-(2m-3)x-m+2\) luôn đồng biến trên \(\mathbb{R}?\)

• Hãy tìm tập xác định của hàm số \(y={{({{x}^{3}}+27)}^{\frac{\pi }{2}}}\)?

• Vườn hoa của một trường học có hình dạng được giới hạn bởi một đường elip có 4 đỉnh \(A,\,B,\,C,\,D\) và 2 đường parabol có các đỉnh lần lượt là \(E,\,F\) (phần tô đậm của hình vẽ bên). Hai đường parabol có cùng trục đối xứng \(AB\), đối xứng nhau qua trục \(CD\), hai parabol cắt elip tại các điểm \(M,\,N,\,P,\,Q\). Biết \(AB=8\,m,\,CD=6\,m, \) \(MN=PQ=3\sqrt{3}\,m,\,EF=2\,m\). Chi phí để trồng hoa trên vườn là \(300.000\)đ/\({{m}^{2}}\). Hỏi số tiền trồng hoa cho cả vườn gần nhất với số tiền nào dưới đây?

  

• Gọi \(m,M\) lần lượt là GTNN, GTLN của hàm số \(y=x-\ln x\) trên đoạn \(\left[ \frac{1}{2};e \right]\). Tính giá trị của \(M-m\)?

• Cho hình chóp \(S.ABC\) có đáy là tam giác đều cạnh bằng \(a\), cạnh \(SA\) vuông góc với mặt đáy và \(SA=2a\). Gọi \(M\) là trung điểm của cạnh \(SC\), tính côsin góc \(\varphi \) giữa đường thẳng \(BM\) và mp \(\left( ABC \right)\)?

• Giá trị cực tiểu của hàm số sau \(y=-{{x}^{3}}+3x+4\)?

• Cho hàm đa thức bậc bốn \(y=f(x)\) có đồ thị như hình:

  

  Khẳng định nào đúng?