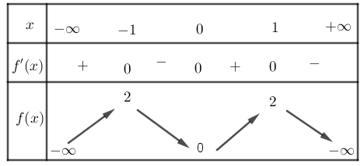
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có BBT như sau:
Số nghiệm thuộc khoảng \(\left( -\infty ;\ln 2 \right)\) của phương trình \(2020f\left( 1-{{e}^{x}} \right)-2021=0\) là?
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
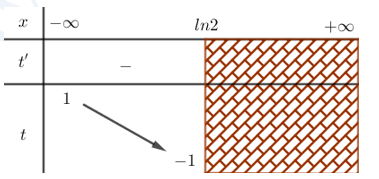
Báo saiĐặt \(t=1-{{e}^{x}}\), \({t}'=-{{e}^{x}}<0,\forall x\in \mathbb{R}\), phương trình \(2020f\left( 1-{{e}^{x}} \right)-2021=0\) trở thành
\(2020f\left( t \right)-2021=0\Leftrightarrow f\left( t \right)=\frac{2021}{2020}\)
\(\Leftrightarrow \left[ \begin{matrix} t={{t}_{1}}, & {{t}_{1}}\in \left( -\infty ;-1 \right) & {} & {} \\ t={{t}_{2}}, & {{t}_{2}}\in \left( -1;0 \right) & {} & {} \\ t={{t}_{3}}, & {{t}_{3}}\in \left( 0;1 \right) & {} & {} \\ t={{t}_{4}}, & {{t}_{4}}\in \left( 1;+\infty \right) & {} & {} \\ \end{matrix} \right.\)
Ta có
Các phương trình \(t={{t}_{1}}\), \(t={{t}_{4}}\) không có nghiệm \(x\) thuộc khoảng \(\left( -\infty ;\ln 2 \right)\)
Mỗi phương trình \(t={{t}_{2}}\), \(t={{t}_{3}}\) có một nghiệm \(x\) thuộc khoảng \(\left( -\infty ;\ln 2 \right)\).
Vậy phương trình đã cho có hai nghiệm \(x\) thuộc khoảng \(\left( -\infty ;\ln 2 \right)\).
Chọn B
Đề thi thử tốt nghiệp THPT môn Toán năm 2023-2024
Trường THPT Trần Cao Vân