Cho hàm số \(y=f(x)\) có đạo hàm là \({f}'(x)=(2-x){{\left( {{x}^{3}}-{{x}^{2}}-m \right)}^{2021}},\forall x\in \mathbb{R}\). Có bao nhiêu giá trị nguyên thuộc khoảng \((-2021 ; 2022)\) của tham số \(\mathrm{m}\) để hàm số \(g(x)=f\left(x^{2}-2\right)+\frac{1}{2} x^{4}-4 x^{2}+2022\) có đúng 5 điểm cực trị?
Suy nghĩ trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai\(g(x)=f\left( {{x}^{2}}-2 \right)+\frac{1}{2}{{x}^{4}}-4{{x}^{2}}+2022\)\( \Rightarrow {g}'(x)=2x.{f}'\left( {{x}^{2}}-2 \right)+2{{x}^{3}}-8x.\)
\({g}'(x)=0.\)
\(\Leftrightarrow \left[ \begin{align} & x=0 \\ & {f}'\left( {{x}^{2}}-2 \right)+{{x}^{2}}-4=0 \\ \end{align} \right.\)
\({f}'(x)=(2-x){{\left( {{x}^{3}}-{{x}^{2}}-m \right)}^{2021}}\)\( \Rightarrow {f}'\left( {{x}^{2}}-2 \right)=\left( 4-{{x}^{2}} \right){{\left( {{\left( {{x}^{2}}-2 \right)}^{3}}-{{\left( {{x}^{2}}-2 \right)}^{2}}-m \right)}^{2021}}\)\({f}'\left( {{x}^{2}}-2 \right)+{{x}^{2}}-4=0\)\( \Leftrightarrow \left( {{x}^{2}}-4 \right)\left[ 1-{{\left( {{\left( {{x}^{2}}-2 \right)}^{3}}-{{\left( {{x}^{2}}-2 \right)}^{2}}-m \right)}^{2021}} \right]=0\)
\(\Leftrightarrow \left[ \begin{align} & {{x}^{2}}-4=0 \\ & 1-{{\left( {{\left( {{x}^{2}}-2 \right)}^{3}}-{{\left( {{x}^{2}}-2 \right)}^{2}}-m \right)}^{2021}}=0 \\ \end{align} \right.\)
\(\Leftrightarrow \left[ \begin{align} & x=2 \\ & x=-2 \\ & {{\left( {{x}^{2}}-2 \right)}^{3}}-{{\left( {{x}^{2}}-2 \right)}^{2}}-m=1 \\ \end{align} \right.\)
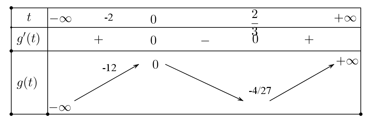
Xét phương trình \({{\left( {{x}^{2}}-2 \right)}^{3}}-{{\left( {{x}^{2}}-2 \right)}^{2}}-m=1\ \left( 1 \right)\).
Đặt \(t={{x}^{2}}-2\Rightarrow t\in \left[ -2;+\infty \right)\).
.PNG)
Ta được phương trình \({{t}^{3}}-{{t}^{2}}=m+1\).
Xét hàm \(g\left( t \right)={{t}^{3}}-{{t}^{2}}\).
Để hàm số có đúng 5 cực trị điều kiện là có đúng 2 nghiệm phân biệt khác 0 và - 2, 2. Với mỗi \(t\in \left( -2;+\infty \right)\) thì phương trình \(t={{x}^{2}}-2\) có hai nghiệm \(x\) phân biệt khác 0.
Do đó, yêu cầu bài toán
\(\Leftrightarrow \left[ \begin{align} & -12< m+1 \le \frac{-4}{27} \\ & 0\le m+1<2022 \\ & m\in Z \\ & m+1\ne 4 \\ \end{align} \right.\)
\(\Leftrightarrow \left[ \begin{align} & -13 < m\le \frac{-31}{27} \\ & -1\le m+1<2021 \\ & m\in Z \\ & m\ne 3 \\ \end{align} \right.\)
\(\Leftrightarrow m\in \left\{ -12;...;-2;-1;...;2;4;...;2020 \right\}\).
Vậy có 2032 giá trị của \(\mathrm{m}\) thỏa mãn yêu cầu bài toán.
Chọn C
Đề thi thử tốt nghiệp THPT môn Toán năm 2023-2024
Trường THPT Trần Cao Vân
Câu hỏi liên quan
-
Thể tích khối tròn xoay tạo thành khi quay quanh trục hoành hình phẳng giới hạn bởi các đường thẳng \(y={{x}^{3}}\) & \(y=2{{x}^{2}}\) là?
-
Cho hàm số \(y=f\left( x \right)\) có BBT như sau:
.png)
Hàm số đã cho đồng biến trên khoảng nào?
-
Cho hàm số \(f\left( x \right)\) thỏa mãn \(f\left( 0 \right)=\frac{2}{3}\) và \(\left( \sqrt{x}+\sqrt{x+1} \right).{f}'\left( x \right)=1,\forall x\ge -1\). Biết \(\int\limits_{0}^{1}{f\left( x \right)dx}=\frac{a\sqrt{2}+b}{15}\) với \(a,b\in \mathbb{Z}\). Tính giá trị của \(T=a+b\)?
-
Cho số phức \(z=\frac{5}{2}-\frac{1}{2}i\). Tìm tọa độ điểm \(M\) biểu diễn số phức \(z\) là?
-
Xét tích phân sau đây \(I=\int\limits_{\frac{\pi }{3}}^{\frac{\pi }{2}}{\frac{\sin 2x}{1+\cos x}dx}\). Nếu đặt \(t=\cos x\) thì tích phân \(I\) trở thành?
-
Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật, biết \(BC=2a\) và \(SA\) vuông góc với mặt phẳng đáy. K/c từ \(D\) đến mặt phẳng \(\left( SAB \right)\) bằng?
-
Trong không gian \(Oxyz\), cho đường thẳng \(d:\frac{x-1}{2}=\frac{y+1}{-1}=\frac{z+3}{2}\). Trong các vectơ dưới đây, vectơ nào là vectơ chỉ phương của đường thẳng \(d\)?
-
Họ nguyên hàm của hàm số sau đây \(f\left( x \right)=3{{x}^{2}}-\frac{1}{x}+\frac{2}{{{x}^{2}}}\) là?
-
Xếp ngẫu nhiên \(6\) học sinh nam và \(4\) học sinh nữ quanh 1 bàn tròn. Xác suất để các học sinh nữ luôn ngồi cạnh nhau là?
-
Trong không gian \(Oxyz\), mp \(\left( Oxz \right)\) có phương trình là?
-
Một CSC \(\left( {{u}_{n}} \right)\) có \({{u}_{13}}=8\) và công sai \(d=-3.\) Tìm số hạng thứ 3 của cấp số cộng \(\left( {{u}_{n}} \right)\)?
-
Cho hình lập phương \(ABCD.{A}'{B}'{C}'{D}'\). Góc giữa 2 đường thẳng \(B{A}'\) và \({B}'{D}'\) bằng?
-
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), cạnh bên \(SA=2a\) và vuông góc với mp đáy. Thể tích khối chóp \(S.ABCD\) bằng?
-
Cho số phức \(z\) thỏa mãn rằng \(3z+2\overline{z}={{\left( 4-i \right)}^{2}}\). Mô đun của số phức \(z\) là?
-
Cho hình nón đỉnh \(S\) có bán kính đáy bằng \(5a\). Gọi \(A\) và \(B\) là 2 điểm thuộc đường tròn đáy sao cho \(AB=8a\). Biết mặt phẳng \(\left( SAB \right)\) tạo với đáy một góc \({{60}^{0}}\), diện tích xung quanh \(S\) của hình nón đã cho bằng?
-
Cho hàm số \(y=f\left( x \right)\) có BBT như sau:
Có bao nhiêu giá trị nguyên dương \(m\) để phương trình \(3f\left( x \right)+2m=0\) có \(2\) nghiệm thực phân biệt?
-
Cho hàm số \(y=\,f(x)=\,a{{x}^{3}}+b{{x}^{2}}+cx+d,\,\) \((a,\,b,\,c,\,d\,\in \mathbb{R},\,a\ne \,0)\). Biết đồ thị \((C)\) của hàm số \(y=\,f(x)\) tiếp xúc với trục hoành tại điểm có hoành độ âm. ĐTHS \(y=\,{f}'(x)\) như hình vẽ. Tính diện tích \(S\) của hình phẳng tạo bởi đồ thị \((C)\) và trục hoành?
-
Tính thể tích \(V\) của khối lăng trụ tứ giác đều có chiều cao bằng \(3cm\), cạnh đáy bằng \(5cm\) là?
-
Cho hàm số \(f\left( x \right)\) liên tục trên tập \(\mathbb{R}\) thỏa mãn \(\int\limits_{0}^{1}{f\left( 2x \right)\text{d}x}=-5\). Tính tích phân sau \(I=\int\limits_{0}^{2}{f\left( x \right)\text{d}x}\)?
-
Nguyên hàm của hàm số sau đây \(f(x)={{3}^{x}}-x\) là?
